Streudiagramm und Regressionsgerade in R

1 Anwendungsfall

Ein Streudiagramm mitsamt linearer Regressionsgerade ist im Falle einer einfachen linearen Regression angebracht. Einfach heißt, es existiert nur eine unabhängige Variable (x), um die abhängige Variable (y) zu erklären. Den Fall zweier unabhängigen Variablen und einer abhängigen Variable kann man im dreidimensionalen Raum abbilden – das ist allerdings nicht Gegenstand dieses Beitrages. Ich zeige zwei hier die Möglichkeit der Erstellung mit Bordmitteln von R.

 

In meinem Beispiel unterstelle ich einen Zusammenhang zwischen dem Intelligenzquotient und dem Abiturschnitt. Die Hypothese lautet: Je höher die Intelligenz, desto niedriger (also besser) der Abiturschnitt. Demzufolge ist die unabhängige Variable der Intelligenzquotient (IQ) und die abhängige Variable der Abiturschnitt (Abischni).

 

2 Diagrammerstellung

Ein Streudiagramm ist recht einfach zu erstellen und an die eigenen Bedürfnisse anzupassen, wie ich in diesem Artikel schon gezeigt habe. Zunächst ist der plot()-Befehl wichtig. In ihn werden die beiden Variablen (x und y) hineingegeben. Die x-Variable (hier: IQ) wird zuerst aufgenommen, dann die y-Variable (hier: Abiturschnitt). Zum Kontext: die Variablen sind nicht “attached”, weswegen ich die Datenquelle data_xls samt $ voranstelle:

plot(data_xls$IQ, data_xls$Abischni)

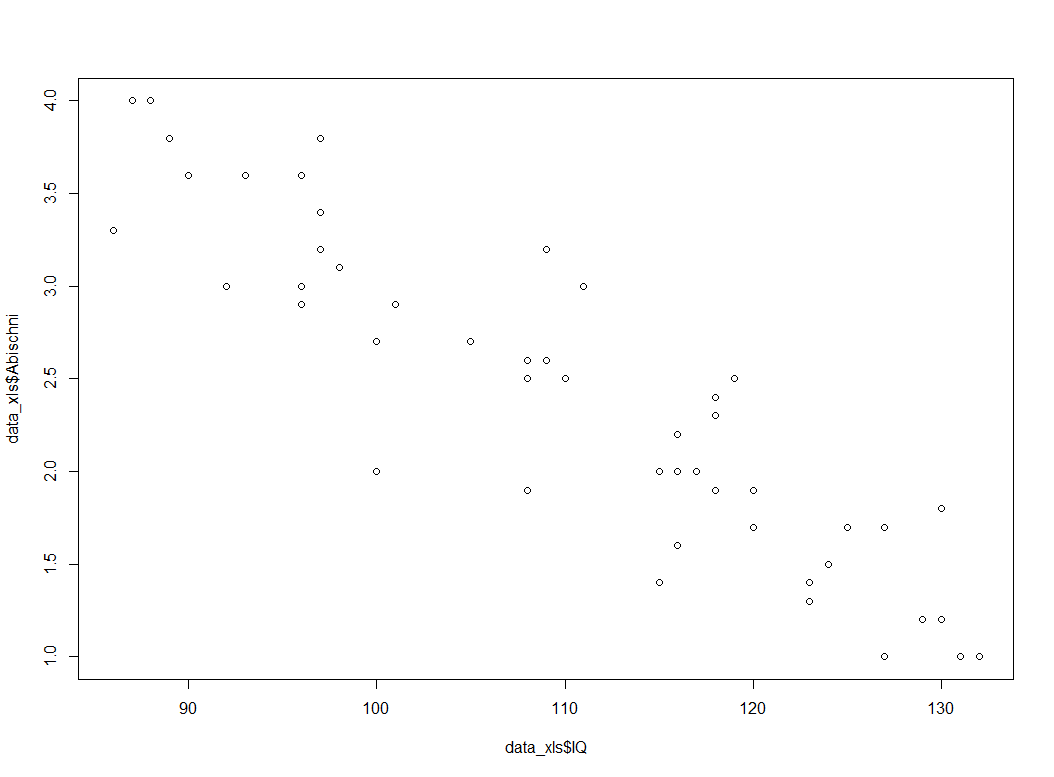Hier ist nun erkennbar, dass die Punkte in etwa in die vermutete Richtung verlaufen. Eine steigender IQ geht mit einem sinkenden Abiturschnitt einher. Nun fehlt allerdings noch die Regressionsgerade. Diese wird mit der abline()-Funktion hinzugefügt. Dazu muss man die Regressionsgleichung formulieren und in diese Funktion einsetzen. Das sieht dann wie folgt aus:

abline(lm(data_xls$Abischni~data_xls$IQ))

 

Dies führt zu folgender Darstellung: 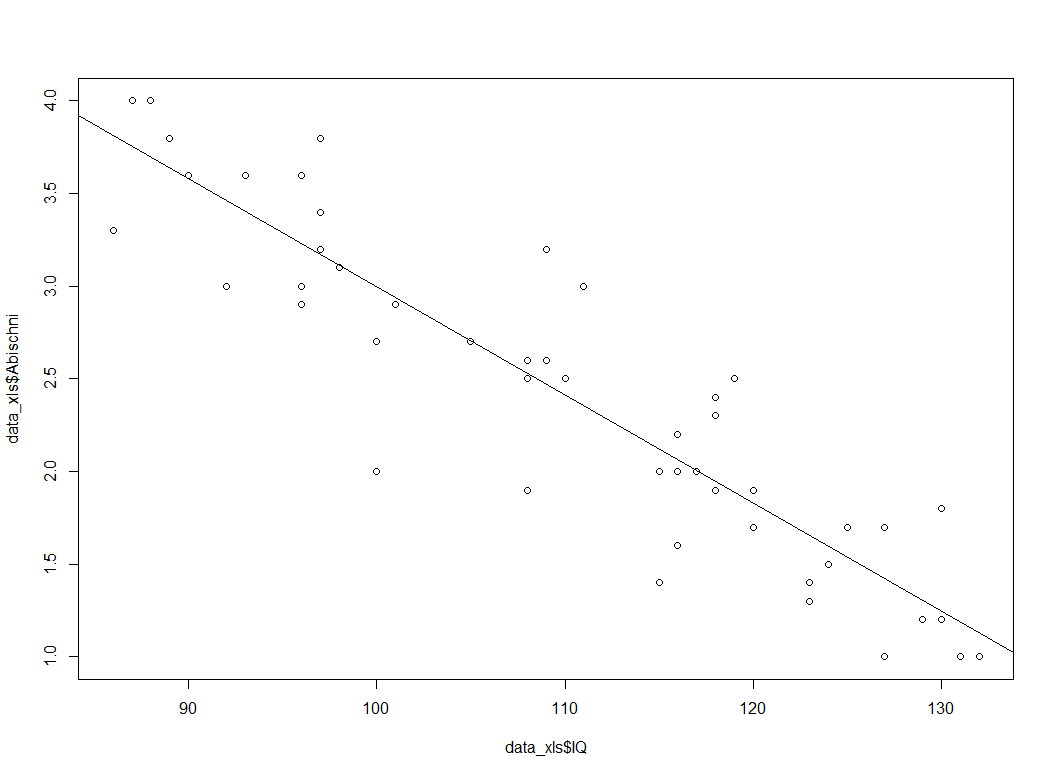Weitere Anpassungen, z.B. Vergabe eines Titels, Anpassung der Achsenbeschriftung usw. sind denkbar und zeige ich in diesem Artikel ausführlicher.

 

3 Einfügen des Bestimmtheitsmaßes (R²)

Hierzu ist es notwendig, dies auch berechnen zu lassen. Dazu bedarf es der Rechnung der Regression und Verweis auf das dadurch erhaltene R². Das Modell modelliere ich mit der lm()-Funktion. Für den Kontext: Mein Modell heißt schlicht “model” und meine Datenquelle ist der Dataframe “data_xls”.

model <- lm(Abischni~IQ, data=data_xls)

Mit der obigen Berechnung wird die Regression berechnet und die Ergebnisse im Vektor "model" gespeichert. Mit der summary()-Funktion kann man sie sich ausgeben lassen. Das Ziel ist jedoch das Streudiagramm mitsamt Regressionsgerade, weswegen ich hierauf verzichte und auf den ausführlichen Beitrag dazu verweise.

 

Danach gebe ich die entsprechende Information in die legend()-Funktion. Dabei verwende ich folgende zusätzliche Argumente:

• "topright" ist die Position der Legende. Es funktionieren auch topleft, bottomright und bottomleft.
• bty="n" ist der Rahmen der Legende und mit ="n" wird er entfernt - er ist mir persönlich zu groß.
• legend = paste 0() setzt das ermittelte Bestimmtheitsmaß in die Legende. Es wird aus dem Vektor "model" entnommen und mit $r.squared adressiert. "R² = " ist lediglich Text, der beliebig gewählt werden kann und dem R²-Wert vorangestellt ist.

  
  legend("topright", bty="n", 
         legend = paste0 ("R² = ", format(summary(model)$r.squared)))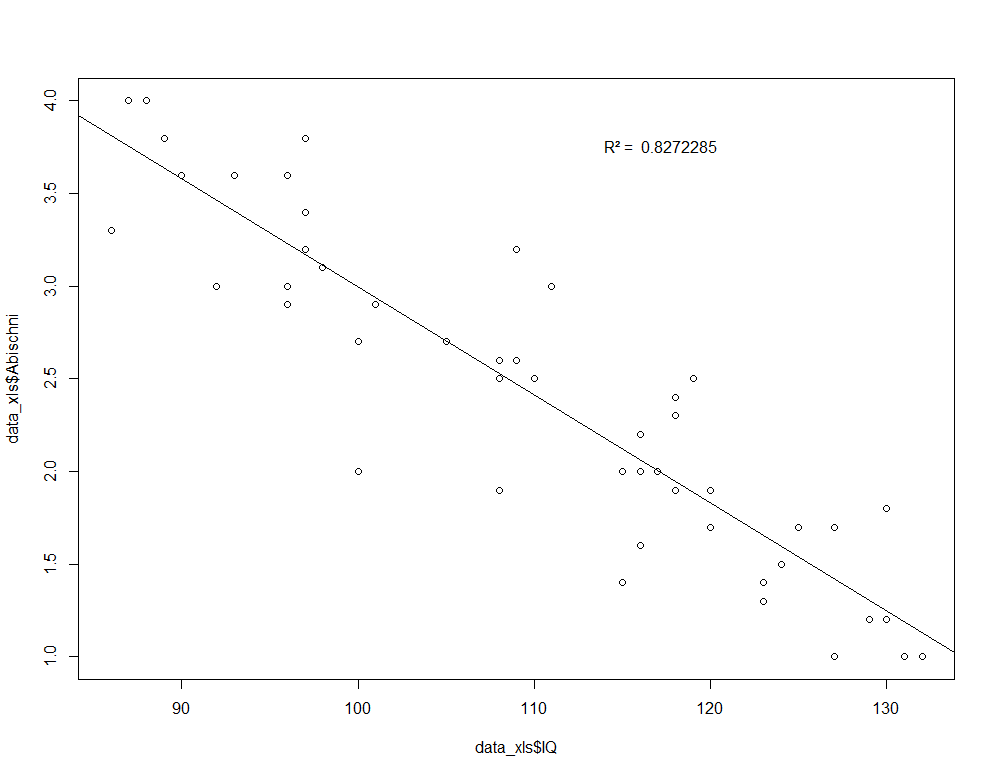
  

  Das sieht dann wie folgt aus:

   

  4 Einfügen der Regressionsgleichung

  Um dies zu erreichen, bedarf es noch einiger weiterer Vorarbeiten. Zunächst sind die Koeffizienten aus dem Vektor "model" zu extrahieren. Ich schreibe sie in einen separaten Vektor namens "koeff":

  
  koeff=coefficients(model)
  

  Anschließend erweitere ich meine obige legend()-Funktion um eine weitere Zeile und verwende die Regressionsgleichung "y = ", round(koeff[2],3), "*IQ ", round(koeff[1],3)". ACHTUNG: ich setze die Regressionsgleichung in die erste Zeile und lasse mir mit der umschließenden round()-Funktion jeweils 3 Nachkommastellen der Konstante (koeff[1]) und des IQ (koeff[2]) mit der angeschlossenen "3" ausgeben. Ganz wichtig ist zudem das "\n" vor dem "R²". Das führt zu einem Zeilenumbruch, also dass die beiden Informationen auf zwei Zeilen verteilt werden.

  
  legend("topright", bty="n", 
         legend = paste0 ("y = ", round(koeff[1],3), "+ IQ*", round(koeff[2],3),
         "\nR² = ", format(summary(model)$r.squared)))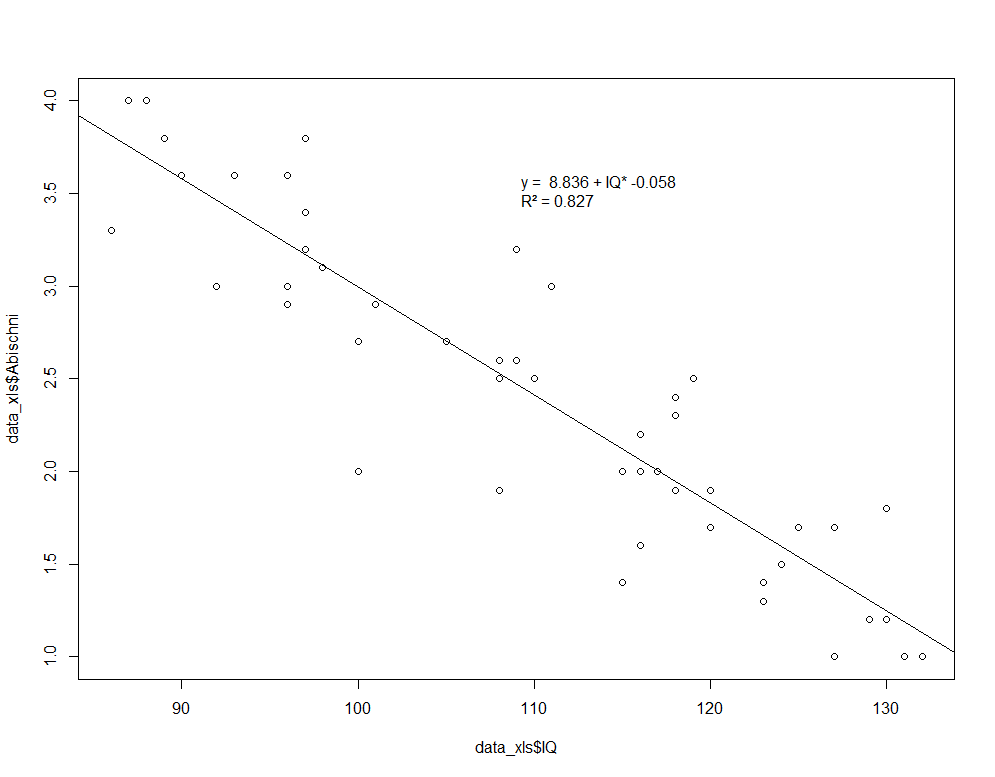
  

  

   

  5 Gesamter Code

  Den Code kann man noch etwas zusammenkürzen, was ich hier getan habe. Der vorangegangene Code sollte v.a. zeigen, wie einzelne Aspekte gelöst werden, wenn schon gewisse Teile existieren oder noch fehlen.

  
  # Modell aufstellen
  model <- lm(Abischni~IQ, data=data_xls)
  
  #Streudiagramm plotten
  plot(data_xls$IQ, data_xls$Abischni)
  
  #Regressionsgerade einzeichnen
  abline(model)
  
  #Regressionskoeffizienten ermitteln
  koeff=coefficients(model)
  
  #Regressionsgleichung aufstellen
  eq = paste("y = ", round(koeff[1],3), "+ IQ*", round(koeff[2],3))
  
  # Bestimmtheitsmaß ermitteln
  r2 = paste("\nR² =", round(summary(model)$r.squared,3))
  
  # Legende einfügen
  legend("topright", bty="n", 
         legend = paste0 (eq, r2))
  

   

  6 Videotutorial

  Dieses Video auf YouTube ansehen.

   

  7 Datensatz zum Download

  Datei als .zip zum Download

  Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.