Inhaltsverzeichnis
1 Ziel der einfachen linearen Regression
Eine einfache lineare Regressionsanalyse hat das Ziel eine abhängige Variable (y) mittels einer unabhängigen Variablen (x) zu erklären. Es ist ein quantitatives Verfahren, das zur Prognose der abhängigen Variable dient.
Die einfache lineare Regression testet auf Zusammenhänge zwischen x und y. Dies kann man auch grafisch darstellen, wie ich in diesem Artikel zeige. Für mehr als eine x-Variable wird die multiple lineare Regression verwendet. Für SPSS und Excel, schaut euch die jeweiligen Artikel an. Im Vorfeld der Regressionsanalyse kann zudem eine Filterung vorgenommen werden, um nur einen gewissen Teil der Stichprobe zu untersuchen, bei dem man am ehesten einen Effekt erwartet.
2 Voraussetzungen der einfachen linearen Regression
Die wichtigsten Voraussetzungen sind:
- Linearer Zusammenhang zwischen x und y-Variable – wird streng genommen ja mit der Regression ersichtlich, ob das der Fall ist oder nicht – zur Not eine Korrelation bzw. Streudiagramm
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme
- Skalenbildung für latente Konstrukte, im Vorfeld evtl. Rekodierung von Items und Reliabilitätsprüfung
- Homoskedastizität – homogen streuende Varianzen des Fehlerterms (grafische Prüfung oder analytische Prüfung)
- keine Autokorrelation – Unabhängigkeit der Fehlerterme (Vorsicht bei Durbin-Watson-Test!)
- Optional: fehlende Werte definieren, fehlende Werte identifizieren und fehlende Werte ersetzen
- Kontrolle für einflussreiche Fälle bzw. “Ausreißer”
3 Durchführung der einfachen linearen Regression in R
Hinweise vor der Durchführung:
- Es sollten Hypothese(n) formuliert sein.
Bei der einfachen linearen Regression eignen sich “Je …, desto …“-Formulierungen sehr gut.
Im hier zu rechnenden Beispiel: “Je größer die Menschen, desto schwerer sind sie.“ - Sofern noch nicht gesschehen, sollte man mit dem Einlesen der Daten beginnen.
- Die Installation zusätzlicher Pakete ist nicht notwendig.
3.1 Visualisierung mittels Punkt-/Streudiagramm
Bei nur einer unabhängigen Variable lässt sich der Zusammenhang im zweidimensionalen Raum darstellen. Jeder Kombination von x- und y-Variable, in meinem Beispiel Größe und Gewicht, lässt sich als Datenpunkt in einem Diagramm abbilden.
Hierzu reicht die einfache plot()-Funktion. Eine Regressionsgerade kann auch eingefügt werden und optisch ansprechendere Streudiagramme mit ggplot2 sind auch möglich. Für unseren Zweck der einfachen Visualisierung reicht ein ganz einfaches Streudiagramm aus.
In die plot()-Funktion werden die beiden Variablen per Komma getrennt eingefügt. Die Nennung des Dataframes (hier: df) ist zusätzlich notwendig:
plot(df$Größe, df$Gewicht)
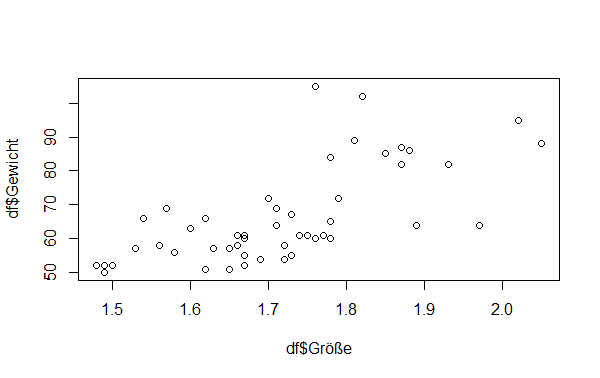
Ein positiver Zusammenhang zwischen Größe und Gewicht ist hier erkennbar und bekräftigt unsere bereits aufgestellte Vermutung zunächst. Zur Bekräftigung der Hypothese ist aber eine analytische Prüfung durchzuführen, was nachfolgend gezeigt wird.
3.2 Rechnen der einfachen linearen Regression
Nun geht es an die Modelldefinition. In meinem Beispiel versuche ich das Gewicht in kg von Probanden durch deren Größe in m zu erklären. Demzufolge ist die abhängige (y-)Variable das Gewicht in kg und die unabhängige (x-)Variable die Größe in m.
Zur einfachen linearen Regression verwendet man die lm()-Funktion. lm steht hierbei für linear model. Ich definiere mir ein Modell mit dem Namen “model”. Hierin soll Gewicht erklärt werden und wird an den Anfang in der Klammer gestellt, gefolgt von ~ und der erklärenden Variable Größe. Die Daten kommen aus dem Dataframe “df”, weshalb ich das “data=“-Argument noch angefügt habe.
Mit der summary()-Funktion lasse ich mir die Ergebnisse der Berechnung von “model” ausgeben.
model <- lm(Gewicht ~ Größe, data=df)
summary(model)
Die Ausgabe ist im nächsten Schritt zu interpretieren.
4 Interpretation der Ergebnisse der einfachen linearen Regression in R
4.1 Ergebnisse der Regressionsmodellschätzung
Call:
lm(formula = Gewicht ~ Größe, data = df)
Residuals:
Min 1Q Median 3Q Max
-19.893 -7.674 -1.171 5.074 35.822
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -54.15 19.12 -2.832 0.00669 **
Größe 70.07 11.11 6.306 7.9e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 10.45 on 49 degrees of freedom
Multiple R-squared: 0.448, Adjusted R-squared: 0.4367
F-statistic: 39.76 on 1 and 49 DF, p-value: 7.895e-08
So sieht der Output aus. Die Interpretation erfolgt schrittweise unter dem jeweiligen Output.
4.2 Erklärungsbeitrag des Regressionsmodells – F-Test
F-statistic: 39.76 on 1 and 49 DF, p-value: 7.895e-08
Man beginnt ganz unten bei der F-Statistik. Schreibweise: F (1,49) = 39,76; p < 0,001.
Auf der Signifikanz (p-Wert) liegt das Hauptaugenmerk. Sie sollte einen möglichst kleinen Wert (<0,05) haben. Wenn dem so ist, leistet das Regressionsmodell einen Erklärungsbeitrag.
7,895e-08 ist eine andere Schreibweise für 0,00000007895. Also im Beispiel deutlich unter 0,05. Das Modell leistet in diesem Falle einen signifikanten Erklärungsbeitrag und es kann mit der Interpretation der weiteren Ergebnisse fortgefahren werden.
Achtung: Ist die Signifikanz über 0,05, leistet das Regressionsmodell keinen signifikanten Erklärungsbeitrag und das Verfahren bzw. die weitere Interpretation ist abzubrechen,
4.3 Güte des Regressionsmodells
Multiple R-squared: 0.448, Adjusted R-squared: 0.4367
Die Güte des Modells der gerechneten Regression wird anhand des Bestimmtheitsmaßes R-Quadrat (R²) abgelesen. Das R² (Multiple R-Squared) ist standardmäßig zwischen 0 und 1 definiert. R² gibt an, wie viel Prozent der Varianz der abhängigen Variable (hier: Gewicht) erklärt werden. Ein höherer Wert ist hierbei besser.
Im Beispiel erklärt das Modell 44,8% der Varianz, da das (Multiple R-sqaured) R² = 0,448 ist.
Das korrigierte R² (Adjusted R-squared) spielt in einer einfachen linearen Regression keine Rolle und findet nur bei einer multiplen linearen Regression Anwendung.
Die Frage, was ein gutes R² ist, kann pauschal nicht beantwortet werden. Man sollte hierfür ähnliche Studien und deren R² hearnziehen. Existieren diese nicht, kann man evtl. vorhandene fachspezifische Grenzen zur Einordnung verwenden.
4.4 Signifikanz und Größe der Koeffizienten
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -54.15 19.12 -2.832 0.00669 **
Größe 70.07 11.11 6.306 7.9e-08 ***
- Der Regressionskoeffizient (hier: Größe) sollte einen hinreichend kleinen p-Wert (p < 0,05) haben. Damit wird das Risiko reduziert die Nullhypothese fälschlicherweiser abzulehnen. Die Signifikanz von Größe ist mit 7,9e-08 deutlich unter 0,05 und somit kann geschlossen werden, dass es sehr unwahrscheinlich ist, dass die Größe einen zufälligen Einfluss auf das Gewicht hat.
Mit anderen Worten: in der vorliegenden Stichprobe konnte ein Einfluss von Größe auf Gewicht beobachtet werden. - Unter “Estimate” ist der interpretierbare Effekt dieses Koeffizienten zu sehen. Im Regressionsmodell steht zunächst in der ersten Zeile der (Intercept). Das ist die sog. Konstante (Achsenabschnitt). Deren Signifikanz ist für den Fortgang der Untersuchung nicht relevant. Hier ist nur der Estimate interessant. Und eigentlich ist er auch nur dann interessant, wenn eine Prognose durchgeführt werden soll.
- In der zweiten Zeile steht der Estimate für die Größe. Das ist der Wert, um den sich die abhängige Variable (Gewicht) ändert, wenn die unabhängige Variable um eine Einheit steigt – immer!
Konkret im Beispiel ist es 70,07. Das heißt, dass bei einer Steigerung der Größe um eine Einheit das Gewicht um 70,07 kg zunimmt. Da die Größe in Metern gemessen wurde, ist das plausibel. Ein Meter größer heißt für diesen Datensatz 70,07 kg schwerer. Man kann das auch umrechnen. 1 cm ist ein Hundertstel eines Meters, das heißt bei einem cm mehr Größe steigt das Gewicht um 70,07/100 = 0,7007kg. - Generell gilt: Positive Koeffizienten haben einen positiven Einfluss auf die y-Variable und negative Koeffizienten einen negativen Einfluss.
4.5 Einseitige Testung vs. zweiseitige Testung
Ausführlich zur Formulierung von Hypothesen, die eine einseitige Testung ermöglichen.
Hier in Kurzform:
- Existiert eine Wirkungsvermutung, darf einseitig getestet werden. Dazu ist es notwendig im Vorfeld eine gerichtete Hypothese hergeleitet und formuliert zu haben und eine einseitige Testung auszuweisen.
- Ungerichtet würde die Hypothese lauten: “Größe hat einen Einfluss auf das Gewicht einer Person” – hierbei ist aber nicht klar, ob eine positive oder negative Wirkung einer steigenden Körpergröße auf das Gewicht vorliegt.
- Meist werden Hypothesen gerichtet formuliert, allerdings grundlos zweiseitig getestet.
Ein Beispiel für eine gerichtete Hypothese lautet: “Je größer eine Person, desto schwerer ist sie.” (vgl. zu oben)
- ACHTUNG: wird einseitig getestet, der Koeffizient ist aber umgedreht zur Hypothese, muss jene zwingend verworfen werden.
5 Prognose anhand der Regressionsergebnisse
Die Regressionsgleichung lautet für das Beispiel:
Gewicht in kg = Konstante + Koeffizient der Größe in m * Größe in m:
Gewicht in kg = -54,15 + 70,07*Größe in m
Setzt man z,B. 1,75m als Größe in diese Gleichung ein, erhält man auf Basis des Modells ein geschätztes Gewicht von 68,48 kg.
6 Datensatz zum Download
7 Videotutorials


