Eine lineare Regression kann alle möglichen Skalenniveaus für die unabhängigen Variablen haben. Allerdings muss man bei kategorialen unabhängigen Variablen besonders aufpassen. Was genau zu beachten ist, zeige ich in diesem Artikel.
Beim Einbeziehen von kategorialen (nominalen) Variablen rechnet man typischerweise eine ganz normale multiple lineare Regression. Die Ausnahme ist allerdings die vorher notwendige Dummykodierung der kategorialen Variablen. Zusätzlich sind natürlich die Voraussetzungen der (multiplen) linearen Regression zu erfüllen.
Inhaltsverzeichnis
1 Voraussetzungen der multiplen linearen Regression mit binären Variablen
Die wichtigsten Voraussetzungen sind:
- linearer Zusammenhang zwischen x-Variablen und y-Variable – wird streng genommen ja mit der Regression ersichtlich, ob das der Fall ist oder nicht – zur Not eine Korrelation.
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme
- Skalenbildung für latente Konstrukte, im Vorfeld evtl. Rekodierung von Items und Reliabilitätsprüfung
- Homoskedastizität – homogen streuende Varianzen des Fehlerterms (grafische Prüfung oder analytische Prüfung)
- keine Autokorrelation – Unabhängigkeit der Fehlerterme (Vorsicht bei Durbin-Watson-Test!)
- keine Multikollinearität – übermäßige Korrelation der unabhängigen Variablen miteinander
- Optional: fehlende Werte definieren, fehlende Werte identifizieren und fehlende Werte ersetzen
- Kontrolle für einflussreiche Fälle bzw. “Ausreißer”
2 Durchführung der linearen Regression mit kategorialen Variablen in R
Im Vorfeld ist unbedingt eine Dummykodierung der kategorialen unabhängigen Variablen vorzunehmen. In meinem Beispiel wirkt die Wohnsituation auf die Zufriedenheit. Wohnsituation wird mit den Kategorien “Wohnung”, “Reihenhaus” und “Einfamilienhaus” gemessen. Diese Variable mit ihren drei Ausprägungen ist in drei Dummyvariablen umzuwandeln. Das zeige ich im Artikel Dummyvariablen in R erstellen. Ich empfehle den Artikel wärmstens, um die Codierung der Dummyvariablen auf Basis der kategorialen Variable zu verstehen.
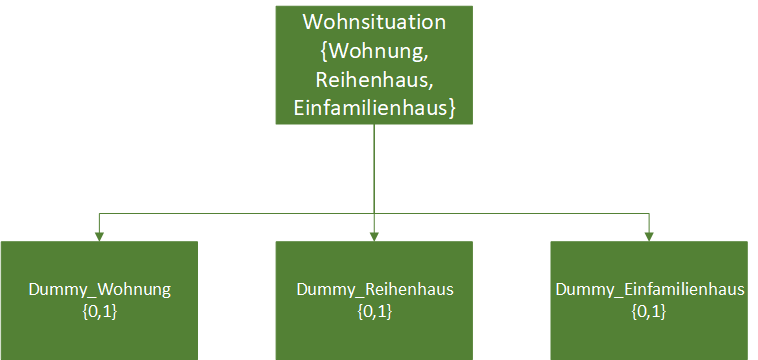
Wie im oberen Bild erkennbar, ist jede Ausprägung mit einer extra Variable hinterlegt. “0” bedeutet, dass diese Wohnsituation nicht vorliegt. “1” heißt, sie liegt vor. Technisch braucht man nur 2 statt 3 Dummyvariablen, um den Effekt zu schätzen. Die nicht in die Regression aufgenommene Dummyvariable ist automatisch die Referenzkategorie. Im Beispiel nehme ich die Dummyvariablen Reihenhaus und Einfamilienhaus auf. Somit ist die Wohnung automatisch meine Referenzkategorie.
Über die lm()-Funktion: Hier versuche ich als abhängige Variable die Zufriedenheit zu erklären. Dafür nutze ich nur die unabhängige Variablen Wohnsituation. Weitere ordinale oder metrische Variablen sind denkbar – deren Interpretation bespreche ich hier. Wohnsituation ist dummy-codiert.
model <- lm(data = data_xls, Zufriedenheit~ DRHaus + DEHaus)
summary(model)
Weitere notwendige Voraussetzungsprüfungen führe ich an dieser Stelle nicht explizit auf. Die entsprechenden Tests sind im obigen Abschnitt Voraussetzungen verlinkt.
3 Interpretation der Ergebnisse der linearen Regression mit kategorialen Variablen in R
Call:
lm(formula = Zufriedenheit ~ DRHaus + DEHaus, data = data_xls)
Residuals:
Min 1Q Median 3Q Max
-23.333 -12.287 1.667 9.713 24.273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 102.727 3.905 26.309 <2e-16 ***
DRHaus 6.606 5.141 1.285 0.2049
DEHaus 10.513 4.686 2.244 0.0295 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.95 on 48 degrees of freedom
Multiple R-squared: 0.09544, Adjusted R-squared: 0.05775
F-statistic: 2.532 on 2 and 48 DF, p-value: 0.09006
Sofern die o.g. Voraussetzungen erfüllt sind, sind drei Dinge bei der Ergebnisinterpretation bei der Regression mit kategorialen Variablen besonders wichtig.
3.1 F-Statistik bzw. F-Test
F-statistic: 2.532 on 2 and 48 DF, p-value: 0.09006
Die F-Statistik sollte einen signifikanten Wert (<0,05) ausweisen. Wenn das zutriftt, leistet das Regressionsmodell einen signifikanten Erklärungsbeitrag. Im obigen Beispiel ist die Signifikanz mit 0,09 zu hoch und damit ist eigentlich das Verfahren abzubrechen. Warum? Weil das Regressionsmodell mit seinen unabhängigen Variablen schlicht die abhängige Variable nicht besser erklären kann als ohne. Das ist häufig ein Hinweis auf keine ausreichende Linearität des Zusammenhanges, sofern es eine hinrechend große Stichprobe (n>30) ist.
3.2 Die Modellgüte
Multiple R-squared: 0.09544, Adjusted R-squared: 0.05775
Die Modellgüte wird bei einer multiplen Regression - auch mit Dummyvariablen - typischerweise anhand des korrigierten R-Quadrat (R²) abgelesen (im Beispiel: 0,058). Dies findet man in der Zeile Multiple R-Squared. Korrigiert ist es deswegen, weil mit einer größeren Anzahl an unabhängigen Variablen das normale R² automatisch steigt. Das korrigierte R² kontrolliert hierfür und ist deshalb stets niedriger als das normale R². Sowohl normales als auch korrigiertes R² sind zwischen 0 und 1 definiert. Nur das normale R² (hier 0,095) gibt an, wie viel Prozent der Varianz der abhängigen Variable erklärt werden. Höher ist dabei besser. Bei einem R² von 0,095 werden 9,5% der Varianz der y-Variable erklärt.
3.3 Koeffiziententabelle
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 102.727 3.905 26.309 <2e-16 ***
DRHaus 6.606 5.141 1.285 0.2049
DEHaus 10.513 4.686 2.244 0.0295 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Die Regressionskoeffizienten sollten signifikant (p<0,05) sein. Im Beispiel ist dies nur die Dummyvariable DEHaus, also die Dummyvariable, die für die Ausprägung Einfamilienhaus der kategorialen Variable Einfamilenhaus steht. Achtung: Der nicht standardisierte Koeffizient ist bei ausreichend niedriger Signifikanz im Vergleich zur Referenzkategorie zu interpretieren. Ich hatte die Wohnung als Referenzkategorie gewählt. Somit ist der Koeffizient von DEHaus (10,513) nur in Relation zur Referenzkategorie "Wohnung" zu interpretieren. Da der Koeffizient ein positives Vorzeichen hat, bedeutet das, dass eine in einem Einfamilienhaus lebende Person, verglichen mit einer in einer Wohnung lebenden Person, eine um 10,513 signifikant höhere Zufriedenheit hat. Oder andersherum: Eine Person, die in einer Wohnung lebt, hat eine um 10,513 niedrigere Zufriedenheit, als eine Person, die in einem Einfamilienhaus lebt. Zwischen der Referenzkategorie Wohnung und dem Reihenhaus besteht zwar ein Unterschied von +6,606 bezüglich der Zufriedenheit, allerdings ist diese nicht statistisch signifikant.
3.4 Tausch der Referenzkategorie - Reihenhaus statt Wohnung
Da man im Vorfeld drei Dummyvariablen erstellt hat, kann man nun beliebig die Referenzkategorie tauschen. Nehme ich jetzt beispielsweise das Reihenhaus als Referenzkategorie, habe ich als Dummyvariablen die Wohnung und das Einfamilienhaus und deren Koeffizienten im Output. Die Modellgüte und die F-Statistik (s.o.) ändern sich beim Austausch der Referenzkategorie nicht.
Call:
lm(formula = Zufriedenheit ~ DEHaus + DWohnung, data = data_xls)
Residuals:
Min 1Q Median 3Q Max
-23.333 -12.287 1.667 9.713 24.273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 109.333 3.344 32.698 <2e-16 ***
DEHaus 3.907 4.230 0.924 0.360
DWohnung -6.606 5.141 -1.285 0.205
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.95 on 48 degrees of freedom
Multiple R-squared: 0.09544, Adjusted R-squared: 0.05775
F-statistic: 2.532 on 2 and 48 DF, p-value: 0.09006
Hier ist erkennbar, dass sich keine statistisch signifikanten Unterschiede zwischen der Referenzkategorie Reihenhaus und Wohnung sowie Einfamilienhaus zeigen. Der Unterschied zwischen Wohnung und Reihenhaus war ja bereits in der vorigen Analyse schon offensichtlich. Die Signifikanz ist logischerweise identisch, beim Koeffizienten ist das Vorzeichen aber umgekehrt. Hier ist auch erkennbar, dass zwischen der Referenzkategorie Reihenhaus und dem Einfamilienhaus zwar ein positiver (3,907) aber kein statistisch signifikanter Unterschied besteht. Wäre der Koeffizient signifikant, würde sich eine Person in einem Einfamilienhaus um 3,907 wohler fühlen als in einem Reihenhaus.
4 Videotutorial
5 Datensatz zum Download


