Inhaltsverzeichnis
1 Ziel des Levene-Tests
Ein Levene-Test (in Form eines F-Test) prüft basierend auf der F-Verteilung, ob zwischen zwei oder mehr Gruppen unterschiedliche Varianzen vorliegen oder Varianzgleichheit zwischen ihnen existiert. Hierbei sollten die Gruppen keine stark unterschiedlichen Größen haben, da die F-Statistik für den Test sonst verzerrt ist. Die Nullhypothese lautet, dass sie gleiche Varianzen besitzen. Die Alternativhypothese demzufolge entsprechend, dass sie unterschiedliche Varianzen besitzen. Der Levene-Test kann auch in Excel oder R durchgeführt werden.
2 Voraussetzungen des Levene-Tests
Voraussetzungen für einen F-Test sind 1) in etwa normalverteilte Daten und 2) unabhängige Stichproben/Gruppen. Wie Daten auf Normalverteilung geprüft werden, zeige ich hier.
3 Durchführung des Levene-Tests in SPSS
Konkret gibt es zwei Anwendungsmöglichkeiten. Zum einen im Rahmen der ANOVA, zum anderen im Rahmen des t-Tests bei unabhängigen Stichproben.
3.1 Durchführung des Levene-Tests bei einer ANOVA
Die Durchführung des Levene-Test bei der ANOVA in SPSS geht über Analysieren -> Mittelwerte vergleichen -> Einfaktorielle Varianzanalyse. Unter Optionen muss der Haken bei „Test auf Homogenität der Varianzen“ gesetzt werden. Die Homogenität der Varianzen wird nun berechnet und in folgender Tabelle dargestellt.
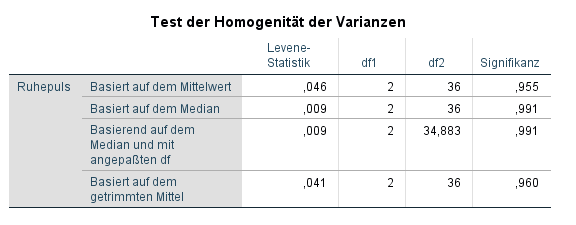
Die wichtige Spalte ist die „Signifikanz“. Da die Nullhypothese bei Gleichheit der Varianzen nicht verworfen werden sollte, sollte die Signifikanz demnach über 0,05 liegen. Dies ist im hier vorliegenden Beispiel der Fall.
- Für den Mittelwert (1. Zeile) ist die Signifikanz des Levene-Tests p = 0,955.
- Für den Median (2. Zeile) ist die Signifikanz p = 0,991. Der Levene-Test basierend auf dem Median gilt als die robustere und daher vorzuziehende Variante.
3.2 Durchführung des Levene-Tests bei einem t-Test bei unabhängigen Stichproben
Die Durchführung des Levene-Test bei einem t-Test bei unabhängigen Stichproben in SPSS geht über Analysieren -> Mittelwerte vergleichen -> t-Test bei unabhängigen Stichproben. Hier muss kein Haken gesetzt werden, es wird direkt folgende Tabelle berechnet.

In ihr ist zu erkennen, ob die Varianzen homogen sind. Dabei ist der erste Teil der Tabelle relevant, der mit Levene-Test der Varianzgleichheit überschrieben ist.

Hier interessiert insbesondere die Signifikanz (hier: 0,628). Die Nullhypothese von Varianzgleichheit konnte hier nicht verworfen werden, weil die Signifikanz über 0,05 liegt. Aufgrund dessen sind die Ergebnisse für den t-Test (obiges Bild) aus der ersten Zeile „Varianzen sind gleich“ zu verwenden und zu interpretieren. Sollte der Fall auftreten, wo die Nullhypothese allerdings abgelehnt werden muss, sind die Ergebnisse der Zeile „Varianzen sind nicht gleich“ (= Welch-Test) zu verwenden und zu interpretieren.
4 Vorsicht – eingeschränkte Verwendbarkeit des Levene-Tests
Die Verwendung des Levene-Tests ist – wie jeder analytische Test – in großen Stichproben zu sensitiv bzw. reagiert auf unbedeutende Abweichungen von Varianzhomogenität zu sensibel. Demzufolge sollten die Ergebnisse kritisch betrachtet werden und im Zweifel bei großen Stichproben lieber auf eine Einschätzung der Varianz an sich geschaut werden (Field, A. (2018), S. 259).
5 Videotutorial
6 Literatur zum Levene-Test
- Field, A. (2018): Discovering Statistics Using SPSS, 5. Auflage, Sage, London.
- Levene, H. (1960): Robust tests for equality of variances. Contributions to probability and statistics. Essays in honor of Harold Hotelling: 278–292, Stanford Univ. Press, Stanford, Calif.
7 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


