1 Ziel der einfaktoriellen Varianzanalyse (ANOVA)
Die einfaktorielle Varianzanalyse (kurz: ANOVA) testet unabhängige Stichproben darauf, ob bei mehr als zwei unabhängigen Stichproben die Mittelwerte einer abhängigen Variable unterschiedlich sind. Die Varianzanalyse in SPSS kann man mittels weniger Klicks durchführen. In Excel und R kann man sie auch durchführen. Sollte eine der folgenden Voraussetzungen nicht erfüllt sein, ist ein Kruskal-Wallis-Test zu rechnen.
Habt ihr einen zweiten Faktor, ist die zweifaktorielle ANOVA zu rechnen. Solltet ihr lediglich eine Kontrollvariable haben, ist eine ANCOVA hingegen die richtige Methode. Sind euer Gruppen/Stichproben abhängig, rechnet ihr den Friedman-Test in SPSS.
2 Voraussetzungen der einfaktoriellen Varianzanalyse (ANOVA)
Die wichtigsten Voraussetzungen sind:
- mehr als zwei voneinander unabhängige Stichproben/Gruppen
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme innerhalb der Gruppen
- Homogene (nahezu gleiche) Varianzen der y-Variablen der Gruppen (Levene-Test über die Ausgabe beim Durchführen der ANOVA)
- Optional: fehlende Werte definiere, fehlende Werte identifizieren und fehlende Werte ersetzen
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Durchführung der einfaktoriellen Varianzanalyse in SPSS (ANOVA)
1) Über das Menü in SPSS: Analysieren -> Mittelwerte vergleichen -> Einfaktorielle Varianzanalyse
ODER
2)Analysieren > Allgemeines lineares Modell > Univariat (*empfohlen)
Als Faktor ist das beiden Gruppen trennende Merkmal/Variable auszuwählen und die Gruppen anhand der Merkmalsausprägungen zu definieren.
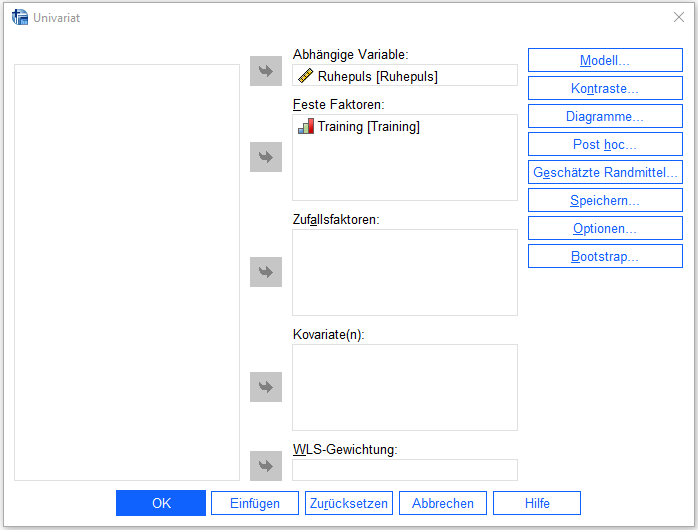
Unter Optionen Deskriptive Statistiken, Homogenitätstests und Schätzungen der Effektgröße auswählen.
Bei Diagramme den Faktor als Horizontale Achse definieren und auf hinzufügen klicken.
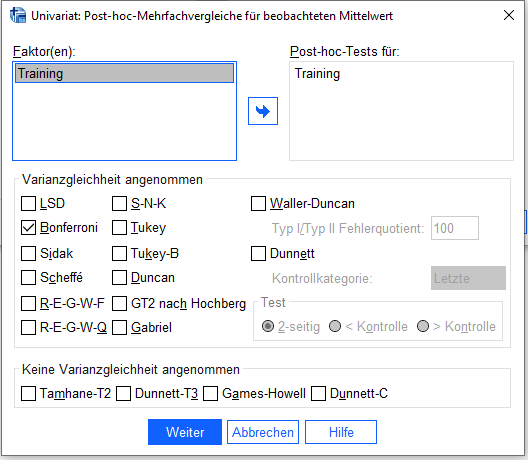
Unter Post hoc den Faktor als “Post-hoc Tests für auswählen” und “Bonferroni” anhaken – dient dem mehrfachen paarweisen Vergleich zwischen den Gruppen. Obwohl Bonferroni aufgrund seiner starken Konservativität nicht unumstritten ist (vgl. Cabin, Mitchell (2000)), ist es zumeist besser konservativer zu testen, um eine Alphafehlerkumulierung zu verhindern.
4 Interpretation der einfaktoriellen Varianzanalyse in SPSS (ANOVA)
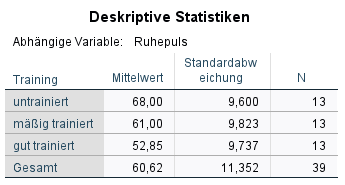
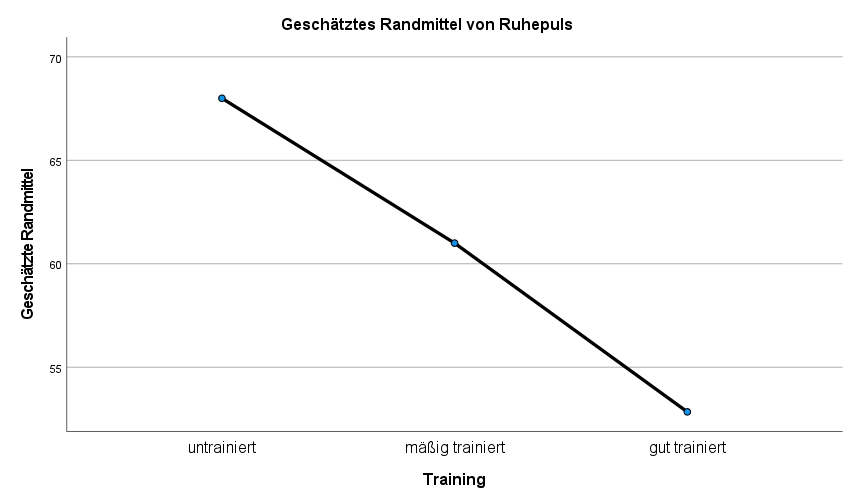
1. Einen ersten Eindruck bzgl. Unterschiede kann man in der Tabelle “Deskriptive Statistiken” und in der Grafik “Geschätzte Randmittel” bekommen. Im Beispiel ist erkennbar, dass sich die drei Gruppen hinsichtlich des Ruhepulses durchaus unterscheiden. Je trainierter, desto niedriger ist der mittlere Ruhepuls. Die Frage, ob dies signifikant ist und welche Gruppen sich unterscheiden, wird nachfolgend beantwortet.
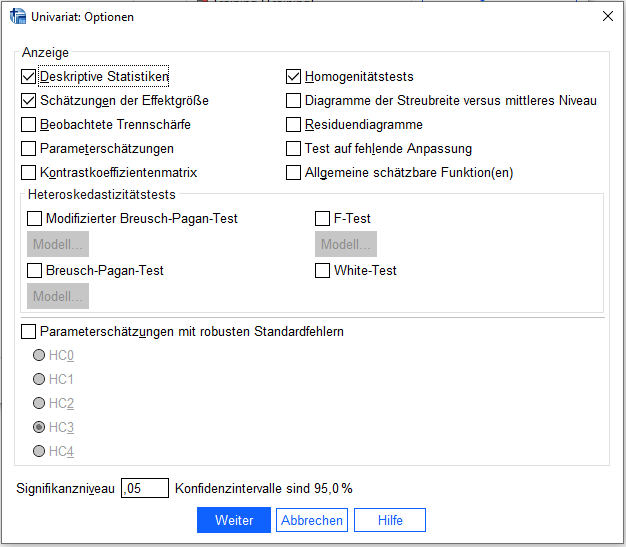
2. Die Voraussetzung der Varianzhomogenität wird mit dem Levene-Test direkt mit den Ergebnissen der einfaktoriellen Varianzanalyse (ANOVA) ausgegeben. Die Nullhypothese lautet hierbei, dass die Varianzen homogen sind. Die Signifikanz sollte demzufolge über 0,05 liegen, damit sie nicht verworfen werden kann und den Stichproben homogene Varianzen bescheinigt werden. Im Beispiel ist die Signifikanz auf Basis aller Lagemaße deutlich über 0,05 und damit liegt Varianzhomogenität vor.
Bzgl. der Lagemaße, wird aufgrund höherer Robustheit “Basiert auf dem Median” empfohlen (George, Mallery (2019), S. 166). Hier ist der Levene-Test mit p = 0,991 deutlich nicht signifikant.
Ist der Levene-Test signifikant, ist eine Welch-ANOVA zu rechnen.
3. Die Tabelle “Tests der Zwischensubjekteffekte” zeigt, ob statistisch signifikante Unterschiede hinsichtlich der Gruppen existieren. Das erkennt man in der Zeile, in der der vorher definierte Faktor (die Trennungsvariable, hier: Training) steht. Ist die Signifikanz kleiner als 0,05, geht man von statistisch signifikanten Unterschieden hinsichtlich der Mittelwerte zwischen den Gruppen aus.
Die Frage zwischen welchen Gruppen signifikante Unterschiede bestehen, beantworten die Post-hoc-Tests (weiter unten).
4. ACHTUNG: Ein 1-seitiges testen ist nicht möglich, da bei mehr als zwei Gruppen nicht gesagt werden kann, welche Gruppe einen größeren oder kleineren Wert hat.
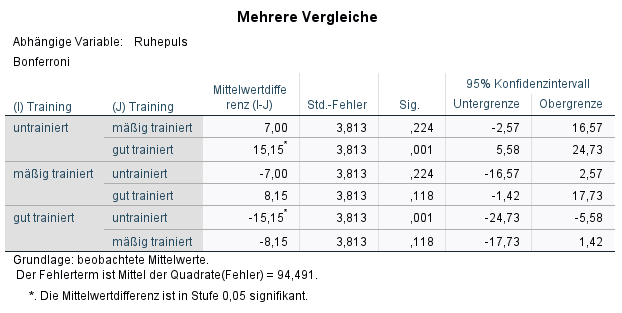
5. In der Tabelle “Mehrere Vergleiche” sieht man die paarweisen Vergleiche, die sog. post hoc-Tests. Hier wird in der ersten Spalte eine Gruppe und in der zweiten Spalte paarweise mit allen anderen Gruppen getestet. Auch hier ist das Hauptaugenmerk auf die Signifikanz zu richten. Wenn zwischen zwei Gruppen ein statistisch signifikanter Unterschied besteht, ist auch hier der Signifikanzwert kleiner als 0,05.
Im Beispiel ist das lediglich zwischen untrainiert und gut trainiert der Fall (p=0,001)
6. Die Effektstärke der ANOVAwird von SPSS in der oberen Tabelle “Tests der Zwischensubjekteffekte” ausgegeben. Sie steht in der Spalte “Partielles Eta-Quadrat” in der Zeile des Faktors (hier: Training). Sie ist manuell umzurechnen und mit Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 284-287 zu beurteilen. Die Berechnung erfolgt über die Formel mit f als Wurzel aus Eta² geteilt durch 1-Eta². Im Beispiel ist sie 0,662.
![\[ f = \sqrt{\frac{\eta^2}{1-\eta^2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-26b0e4363f8a9a93a22800043d6aac50_l3.png "Rendered by QuickLaTeX.com")
Ab 0,1 ist es laut Cohen(1988) ein schwacher Effekt, ab 0,25 ein mittlerer und ab 0,4 ein starker Effekt. Im Beispiel liegt 0,662 deutlich über der Grenze zum starken Effekt. Es ist demzufolge ein starker Effekt für die ANOVA.
ACHTUNG: Je nach Kontext ist es sinnvoller eine Effektstärke für den jeweils signifikanten paarweisen Vergleich zu ermitteln. Hierzu berechnet man für die signifikanten Vergleiche einfach einen t-Test bei unabhängigen Stichproben. Ab SPSS 27 wird die Effektstärke für jenen t-Test direkt ausgegben, vorher muss man es manuell berechnen, was der verlinkte Artikel aber ebenfalls zeigt.
5 Beispieldatensatz
6 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
7 Literatur
- Cabin, R. J., & Mitchell, R. J. (2000). To Bonferroni or not to Bonferroni: when and how are the questions. Bulletin of the ecological society of America, 81(3), 246-248.
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Hillsdale, N.J: L. Erlbaum Associates.
- George, D., & Mallery, P. (2019). IBM SPSS Statistics 26 Step by Step: A Simple Guide and Reference. Routledge.
