1 Ziel des t-Test bei unabhängigen Stichproben in SPSS
Der t-Test für unabhängige Stichproben testet, ob bei zwei unabhängigen Stichproben die Mittelwerte unterschiedlich sind. Für abhängige Stichproben ist der t-Test für verbundene Stichproben zu rechnen. In Excel kann der t-Test für unabhängige Stichproben auch gerechnet werden.
Sind die folgenden Voraussetzungen nicht erfüllt, solltet ihr einen Mann-Whitney-U-Test rechnen.
2 Voraussetzungen des t-Test bei unabhängigen Stichproben in SPSS
Die wichtigsten Voraussetzungen sind:
- zwei voneinander unabhängige Stichproben/Gruppen
- metrisch skalierte y-Variable
- normalverteilte y-Variable innerhalb der Gruppen (in einem separaten Artikel zum Test auf Normalverteilung)
- Homogene (nahezu gleiche) Varianzen der y-Variablen der Gruppen (Levene-Test über die Ausgabe beim Durchführen des t-Test)
- Optional: fehlende Werte definiere, fehlende Werte identifizieren und fehlende Werte ersetzen
- Achtung: Mindeststichprobengröße bedenken – über eine Poweranalyse zu ermitteln
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
3 Durchführung des t-Test bei unabhängigen Stichproben in SPSS
Über das Menü in SPSS: Analysieren -> Mittelwerte vergleichen -> T-Test für unabhängige Stichproben
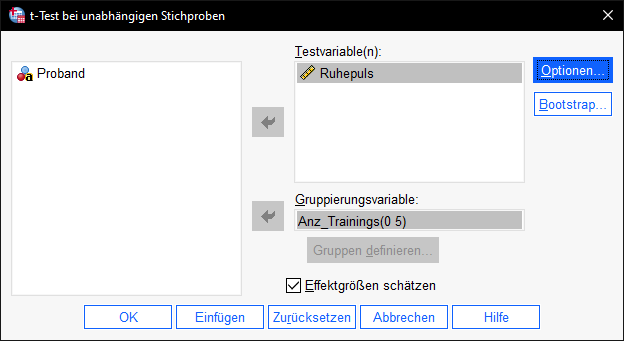
Unter Optionen 95% Konfidenzintervall und “Fallausschluss Test für Test”.
Als Gruppierungsvariable ist das die beiden Gruppen trennende Merkmal/Variable auszuwählen und die beiden Gruppen anhand der Merkmalsausprägungen zu definieren.
4 Ergebnisse des t-Test bei unabhängigen Stichproben in SPSS
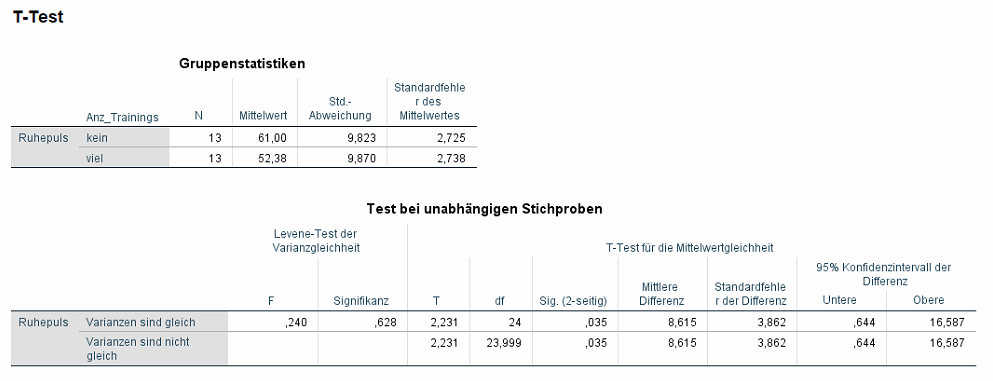
Man erhält zwei Tabellen, die Gruppenstatistiken und die Tabelle für den t-Tets bei unabhängigen Stichproben.
5 Interpretation des t-Test bei unabhängigen Stichproben in SPSS
Statistisch signifikanter Unterschied – ja oder nein?
1. Zunächst kann man im Beispiel an den Gruppenstatistiken erkennen, dass die Gruppe mit keinen Trainings einen Ruhepuls von durchschnittlich 61 hat. Die Gruppe mit vielen Trainings hat einen mittleren Ruhepuls von 52,38. Die Frage ist, ob diese Unterschiede statistisch signifikant sind. Hierzu bedarf es des t-Tests.
2. Bevor allerdings auf den t-Test geschaut werden darf, muss noch die Varianzhomogenität bzw. -gleichheit geprüft werden. Die Voraussetzung der Varianzhomogenität wird mit dem Levene-Test direkt mit den Ergebnissen des t-Test ausgegeben. Die Nullhypothese lautet hierbei, dass die Varianzen homogen sind. Die Signifikanz sollte demzufolge über 0,05 liegen, damit sie nicht verworfen werden kann und den beiden Stichproben homogene Varianzen bescheinigt werden. Die entsprechende Stelle ist mit rot markiert und im Beispiel liegt die Signifikanz beim Test auf Varianzhomogenität deutlich über 0,05 – die Nullhypothese von Varianzhomogenität kann also nicht verworfen werden.
3. Im Falle von Varianzhomogenität spielt nur die Zeile “Varianzen sind gleich” eine Rolle. Der Unterschied ist signifikant, wenn das 95%-Konfidenzintervall den Wert “0” nicht beinhaltet, also beide Intervallgrenzen positiv oder negativ sind. Besonderes Augenmerk liegt auf der Sig. (2-seitig). Ist sie kleiner 0,05, geht man von statistisch signifikanten Unterschieden hinsichtlich der Mittelwerte zwischen den Stichproben aus.
ACHTUNG: Hat man bereits eine Vermutung, dass z.B. eine Stichprobe einen höheren/niedrigeren Wert hat, ist dies eine gerichtete Hypothese und man muss 1-seitig testen. Dazu halbiert man den bei Sig. (2-seitig) erhaltenen Wert und prüft jenen auf Signifikanz. Im Beispiel enthält das 95%-Konfidenzintervall die 0 nicht und entsprechend ist auch die Signifikanz unter 0,05 (= Alpha). Die Signifikanz beträgt nämlich 0,035. und lehnt die Nullhypothese des t-Tests von gleichen Mittelwerten ab. Die Signifikanz sollte im übrigen lieber kleiner als größer sein. Warum? Damit man die Nullhypothese nicht fälschlicheriweiser ablehnt.
Da wir uns jedoch im Vorfeld schon bewusst waren, dass trainiertere Menschen in der Regel einen niedrigeren Ruhepuls haben (siehe deskriptive Statistiken), haben wir eine Wirkungsvermutung bzw. eine gerichtete Hypothese. Wir testen also einseitig und dürfen die Signifikanz sogar halbieren. Sie beträgt dann 0,0175 und ist natürlich immer noch signifikant. ACHTUNG: Ich muss im Vorfeld die Hypothese so formuliert haben, das sie einen einseitigen Test zulässt. Ein nachträgliches Umformulieren ist nicht statthaft – kann aber freilich auch nicht vom Gutachter geprüft werden. 😉
Im Falle von Varianzheterogenität ist die Zeile “Varianzen sind nicht gleich” relevant. Die Interpretation ist analog zu der Erklärung bei 2. “Varianzen sind gleich”. Dazu gibt es noch einen ausführlichen Artikel zum sog. Welch-Test.
6 Die Effektstärke – wie stark ist der Unterschied?
6.1 Cohen’s d ab SPSS 27
Die Effektstärke wird von SPSS erst ab Version 27 ausgegeben. Wie stark sich die beiden Stichproben unterscheiden, wird dabei mit Cohen’s d (bei N>20) oder Hedges’ Korrektur (bei N<20 sowie ungleichen Varianzen) quantifiziert. Dies wird mit SPSS 27 standardmäßig berechnet. Ausführlich zu den Unterschieden zwischen d und korrigiertem g: Grissom, Kim (2012), S. 68f.
Diese Größe wird nun eingeordnet. Laut Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 25-26 ist ein Effekt:
- ab 0,2 klein,
- ab 0,5 mittel und
- ab 0,8 stark.
ACHTUNG: Je nach Disziplin können andere Grenzen gelten. Dies ist im Vorfeld zu prüfen.
6.2 Cohen’s d manuell berechnen
Die Formel findet sich auf S. 20 von Cohen (1988) Statistical Power Analysis: ![\[ d = \frac{\bar{x_{1}}-\bar{x_{2}}}{s}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-5e88e7c39a31e9520d17fe93def179fd_l3.png "Rendered by QuickLaTeX.com")
![\[s = \sqrt{\frac{(n_{1}-1)\cdot s_{1}^{2} + (n_{2}-1)\cdot s_{2}^{2}} {n_{1}+n_{2}-2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-caf462eff0873927a026ce8f5d42c09f_l3.png "Rendered by QuickLaTeX.com")
![\[s = \sqrt{\frac{s_{1}^{2}- s_{2}^{2}}{2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-9f97fe989bd4b4ccefbd3d7b76d01a85_l3.png "Rendered by QuickLaTeX.com")
Im Beispiel sind die Mittelwerte 61 und 52,38 (siehe oben) sowie die gepoolte Standardabweichung 9,85. Eingesetzt in die obige Formel:
![\[ d = \frac{61-52,38}{9,85}} = 0,875 \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-563cf14a1c79748ca812cd9151b39e51_l3.png "Rendered by QuickLaTeX.com")
6.3 Effektstärkemaß r manuell berechnen
Eine dritte Möglichkeit ist die manuelle Berechnung von r sowie die Beurteilung anhand Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81. Cohen selbst merkt aber an, dass die Effektstärkemaße und deren Klassengrenzen nicht 1:1 vergleichbar sind. Vorzuziehen ist Cohen’s d. Die Berechnung von r erfolgt über die Formel mit t² als quadrierter T-Wert und df als degrees of freedom (Freiheitsgrade). ![\[ r = \sqrt{\frac{t^2}{t^2+df}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-ea814ae95eca7b794de9e0f93fef19d1_l3.png "Rendered by QuickLaTeX.com")
Ab 0,1 ist es ein schwacher Effekt, ab 0,3 ein mittlerer und ab 0,5 ein starker Effekt.
Im Beispiel ist der t-Wert 2,231 und die Freiheitsgrade (df) 24. Eingesetzt in die Formel:
![\[ r = \sqrt{\frac{2,231^2}{2,231^2+24}}= 0,414 \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-17f504add46caafc8eeda1a987f240c9_l3.png "Rendered by QuickLaTeX.com")
Das Ergebnis von 0,414 liegt über der Grenze zur mittleren Effektstärke und der Unterschied ist damit lauut Cohen ein mittelstarker Unterschied. Allerdings gibt es neuere Richtlinien bzgl. r, die von Gignac, Szodorai (2016) vorgeschlagen wurden, die bei 0,1 (klein), 0,2 (mittel) und 0,3 (groß) liegen. Demnach wäre der Unterschied im Beispiel ein großer.
Auch hierzu gibt es ein kleines Video auf meinem YouTube-Kanal:
7 Reporting des t-Tests bei unabhängigen Stichproben
Gruppenmittelwerte und Standardabweichungen sind zu berichten. Zusätzlich die t-Statistik mit Freiheitsgraden, der p-Wert und die Effektstärke (Cohens d bzw. Hedges’ Korrektur): t(df)=t-Wert; p-Wert; Effektstärke.Untrainierte Probanden (M = 61; SD = 9,82) haben gegenüber trainierten Probanden (M = 52,38; SD = 9,87) einen signifikant höheren Ruhepuls, t(24) = 2,23; p = 0,035; d = 0,88. Nach Cohen (1992) ist dieser Unterschied groß.
8 Literatur
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. New York, NY: Psychology Press, Taylor & Francis Group
- Cohen, J. (1992). A power primer. Psychological bulletin, 112(1), 155-159.
- Gignac, G. E., & Szodorai, E. T. (2016). Effect size guidelines for individual differences researchers. Personality and individual differences, 102, 74-78.
- Grissom, R. J., & Kim, J. J. (2012). Effect sizes for research: Univariate and multivariate applications. New York: Routledge.
9 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
