1 Ziel der bivariaten Korrelation
Eine bivariate Korrelation untersucht zwei Variablen auf eine (lineare) Beziehung bzw. einen Zusammenhang. Sie versucht die Frage zu beantworten, ob zwischen ihnen ein a) positiver, b) negativer oder c) kein Zusammenhang besteht. Ein Korrelationskoeffizient ist zwischen den Maximalwerten -1 und +1 definiert. -1 ist ein perfekt negativer (linearer) Zusammenhang und +1 ein perfekt positiver (linearer) Zusammenhang. Sollte für eine weitere Variablen kontrolliert werden sollen, ist eine partielle Korrelation zu rechnen.
Interpretation der Fälle a)-c)
a) Wenn der Wert einer Variable größer wird, wird der Wert der anderen Variable ebenfalls größer. Das ist positive Korrelation. Zum Beispiel: Je größer ein Mensch, desto schwerer ist er. Hierbei kann man zusätzlich für das Alter kontrollieren. Meist werden Menschen im Alter etwas schwerer.
b) Wenn der Wert einer Variable größer wird, wird der Wert der anderen Variable kleiner. Das ist negative Korrelation. Zum Beispiel: Je größer der Zuckergehalt der Nahrung, desto weniger gesunde Zähne hat der Mensch. Auch hier kann eine Kontrolle für das Alter einen zusätzlichen Nutzen haben, da auch im Alter die Zähne schlechter werden.
c) Die Werte der Variablen ändern sich scheinbar vollkommen beliebig und es gibt kein Muster wie bei a) oder b). Zum Beispiel: Anzahl Haare und Schuhgröße.
Wichtiger Hinweis: Ein Korrelation kann bestenfalls ein Indiz für einen kausalen Zusammenhang sein. Nur weil eine Korrelation existiert, bedeutet das nicht, dass die eine Variable die andere beeinflusst. Dies würde man theoretisch begründen müssen und die Hypothese entsprechend mit einer einfachen linearen Regression oder multiplen linearen Regression untersuchen.
Beispiel: Das Alter der Königin von England und die Anzahl der Menschen auf der Erde korrelieren sehr stark – weder das eine hat mit dem anderen was zu tun. Dies nennt sich Scheinkausalität, da eine Ursache-Wirkungs-Beziehung zwischen den Variablen nicht existiert und sie nur zufällig korrelieren. Von einer Korrelation sollte also auf keinen Fall auf eine Kausalität geschlossen werden!
Am einfachsten kann eine Korrelation mit einem Streudiagramm bzw. Punktdiagramm veranschaulicht werden.
2 Bivariate Korrelation prüfen: Grafische Methode in SPSS
Zu finden ist das Diagramm über Grafik -> Diagrammerstellung -> Streu-/Punktdiagramm.
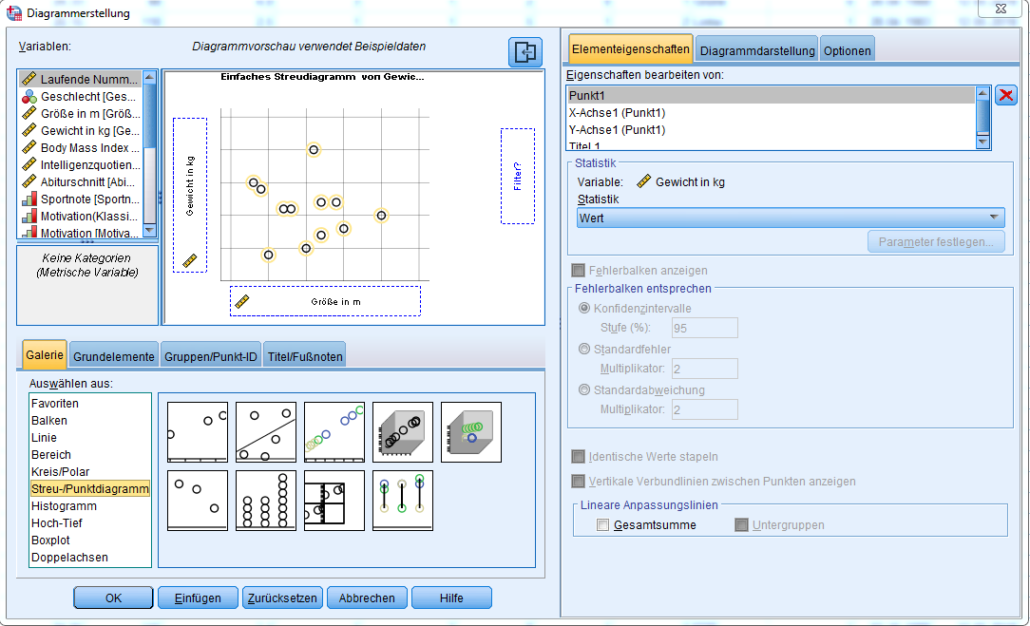
Die zu korrelierenden Variablen sind an die x-Achse und die y-Achse zu ziehen. Über folgende Syntax ist ebenfalls ein Streudiagramm zur bivariaten Korrelation erstellbar. Größe und Gewicht sind durch die zu korrelierenden Variablen zu ersetzen.
GRAPH
/SCATTERPLOT(BIVAR)=Größe WITH Gewicht
/MISSING=LISTWISE.
3 Interpretation des Diagramms
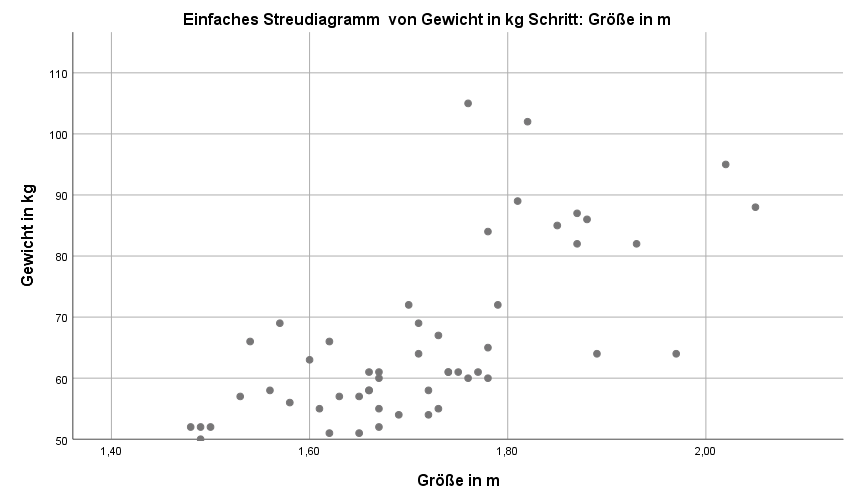
Das folgende Streudiagramm zeigt, dass die “Punktewolke” von links unten nach rechts oben im Diagramm verläuft. Es scheint also, als ob Größe und Gewicht positiv miteinander korrelieren.
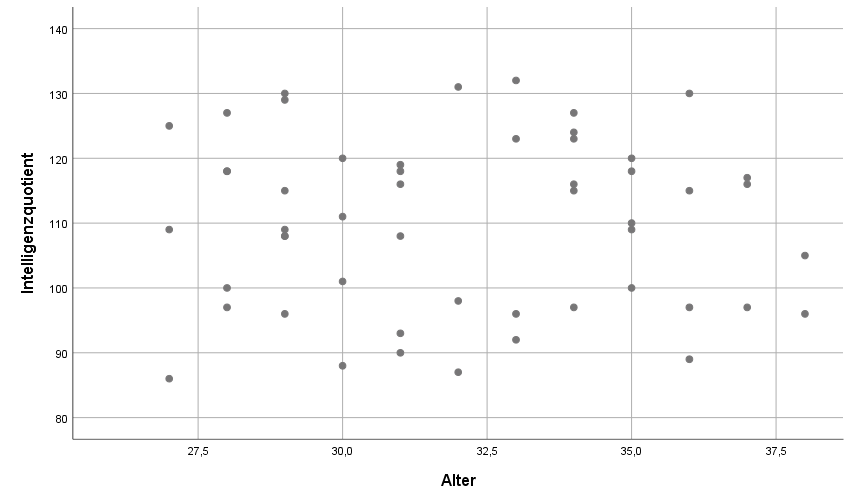
Eine nicht vorhandene Korrelation wäre der IQ und das Alter. Die Punktewolke hat keinen näherungsweisen gerichteten Verlauf. Es scheint total beliebig zu sein.
4 Bivariate Korrelation – Analytisches Vorgehen in SPSS
4.1 Auswahl des Korrelationskoeffizienten
- Die analytische Methode ist aufzurufen über Analyse -> Korrelation -> Bivariat.
- Die zu korrelienden Variablen sind in das Feld Variablen zu übertragen. Unter Korrelationskoeffizienten stehen Pearson, Kendall-Tau-b und Spearman zur Wahl.
- In Abhängigkeit des Skalenniveaus der zu korrelierenden Variablen ist nur einer der Korrelationskoeffizienten die richtige Wahl. Manche Korrelationskoeffizienten sind aber nicht im Dialogfeld aufgeführt und müssen über Deskriptive Statistiken -> Kreuztabellen aufgerufen werden. Folgende Wahl ist zu treffen:
a) beide Variablen sind metrisch: Pearson-Korrelationskoeffizient
Ausnahme: die Variablen sind nicht annähernd normalverteilt. Dann ist der Spearman-Rangkorrelationskoeffizient zu wählen
b) beide Variablen sind ordinal: Spearman
c) beide Variablen sind nominal: Kontigenzkoeffizient, Phi, Cramer-V (über Kreuztabellen)
d) eine Variable ist metrisch, eine ordinal: Kendall-Tau-b, Spearman
e) eine Variable ist nominal, eine ist metrisch: Eta-Koeffizent (über Kreuztabellen)
f) eine Variable ist nominal, eine ist ordinal: Chi²-Unabhängigkeitstest (über Kreuztabellen)
Würde man zwei metrische Variablen (Gewicht und Größe) korrelieren, erhält man folgende Tabelle mit dem Pearson-Korrelationskoeffizient.
Hierzu kann auch folgender Syntax verwendet werden:
CORRELATIONS
/VARIABLES=Größe Gewicht
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE.
4.2 Interpretation einer bivariaten Korrelation in SPSS
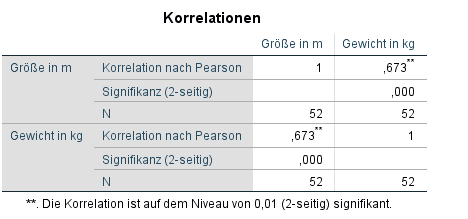
In der Tabelle ist erkennbar, dass die bivariate Korrelation des Pearson-Korrelationskoeffizient positiv (r = 0,673) und statistisch signifikant (p = 0,000 – ausgedrückt auch durch **) ist. Das heißt, dass eine recht starke positive Korrelation von Größe und Gewicht vorliegt.
Würde man Alter und den IQ korrelieren, erhält man folgende Tabelle Korrelationstabelle:
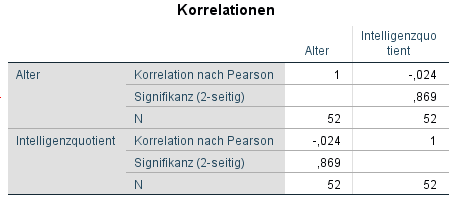
Es ist erkennbar, dass Alter und IQ nur sehr schwach negativ (r = -0,024) korrelieren. Zusätzlich ist die Signifikanz p = 0,869, was bedeutet, dass der negative Koeffizient auch zufällig zustande gekommen sein kann, da er (deutlich) über 0,01 liegt, was als typische Signifikanzschwelle von SPSS verwendet wird.
5 Tipp zum Schluss
Findest du die Tabellen von SPSS hässlich? Dann schau dir mal an, wie man mit wenigen Klicks die Tabellen in SPSS im APA-Standard ausgeben lassen kann.
6 Videotutorial
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
