Inhaltsverzeichnis
1 Ziel der einfaktoriellen Varianzanalyse (ANOVA) mit Messwiederholung
Die einfaktorielle Varianzanalyse (kurz: ANOVA) mit Messwiederholung testet abhängige Stichproben darauf, ob bei mehr als zwei Zeitpunkten die Mittelwerte einer abhängigen Variable unterschiedlich sind. Die Varianzanalyse in SPSS kann man mittels weniger Klicks durchführen.
Habt ihr nur zwei Messwiederholungen, verwendet ihr den t-Test bei abhängigen Stichproben in SPSS. Habt ihr keine Messwiederholungen und wollte dennoch eine einfache ANOVA in SPSS rechnen, braucht ihr mindestens drei Gruppen.
2 Voraussetzungen der einfaktoriellen Varianzanalyse (ANOVA) mit Messwiederholung
Die wichtigsten Voraussetzungen sind:
- mehr als zwei Messungen einer abhängigen Variable, sog. Messwiederholungen
- metrisch skalierte y-Variable
- in etwa normalverteilte Fehlerterme zu den jeweiligen Zeitpunkten (ANOVA ist generell robust gegenüber leichten Verletzungen (vlg. Blanca et al. (2017).
- Sphärizität, also Homoskedastizität (nahezu gleiche) Varianzen der y-Variablen der Gruppen (Levene-Test über die Ausgabe beim Durchführen der ANOVA)
- Optional: fehlende Werte definieren, fehlende Werte identifizieren und fehlende Werte ersetzen
3 Durchführung der einfaktoriellen Varianzanalyse mit Messwiederholung in SPSS (ANOVA)
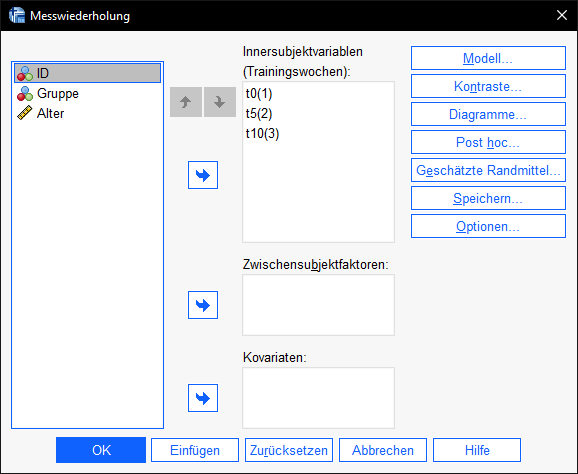
Über das Menü in SPSS: Analysieren -> Allgemeines lineares Modell -> Messwiederholung
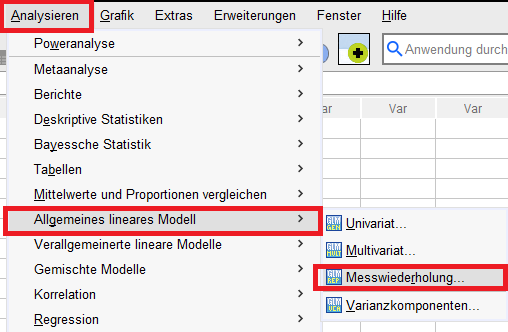
Als erstes sind die Messwiederholungen zu definieren, also der Innersubjektfaktor und die Anzahl der Stufen. Im Beispiel messe ich zu 3 Zeitpunkten den Ruhepuls, dazwischen befinden sich 5 und 10 Trainingswochen im Vergleich zur Ausgangsmessung. Der Innersubjektfaktor bekommt bei mir daher den Namen Trainingswochen und da ich 3 Messzeitpunkte habe, definiere ich 3 Stufen.
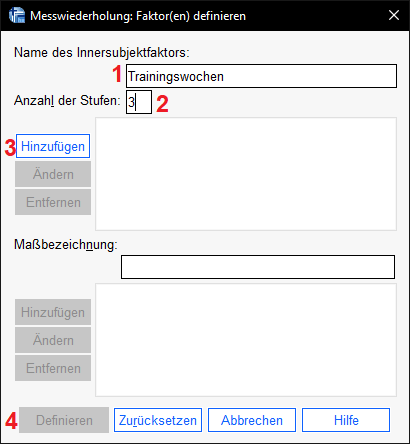
Im Anschluss lege ich die Innersubjektvariablen fest, also die Variablen, die die Messungen beinhalten. In meinem Fall sind das die Variablen t0, t5 und t10.
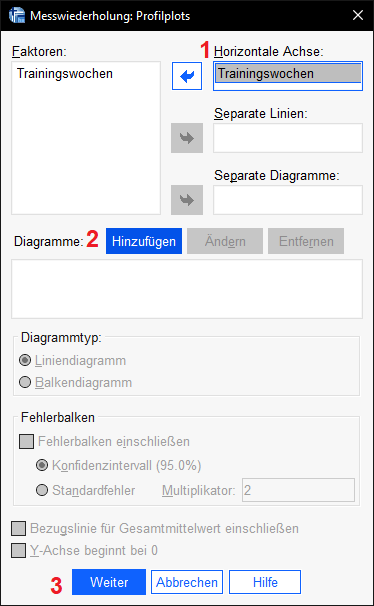
Im Anschluss daran arbeiten wir uns rechts durch die Schaltflächen. Zunächst interessiert uns “Diagramme”. Hier wählen wir den (Innersubjekt)Faktor aus und schieben ihn auf die “Horizontale Achse”, klicken hinzufügen und dann auf weiter.
Als nächstes ist im Menü “Geschätzte Randmittel” auszuwählen. Hier definieren wir den post-Hoc-Test. Wir versuchen damit, wie bei Mehrfachvergleichen auf derselben Stichprobe üblich, den Alphafehler kumulieren zu lassen. Wir wählen also Haupteffekte vergleichen und wählen dann Bonferroni aus und wählen weiter.
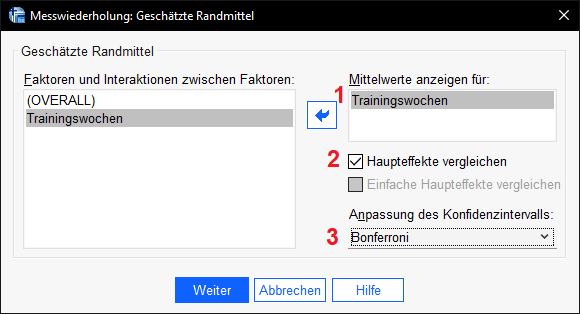
Schließlich gehen wir noch in “Optionen” und wählen “Deskriptive Statistiken” sowie “Schätzungen der Effektgröße” aus.
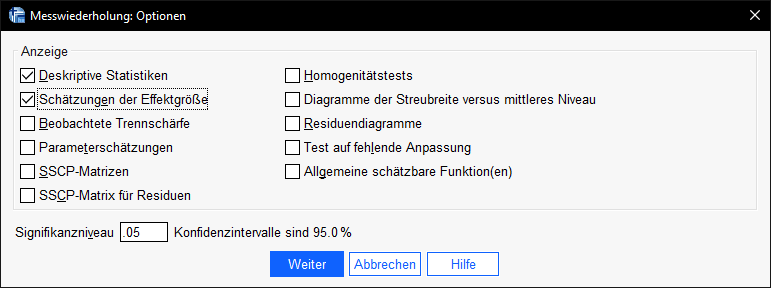
Wenn auch das geschafft ist, kann die ANOVA mit Messwiederholung von SPSS gerechnet werden und wir schauen uns die Ergebnisse an und interpretieren sie im nächsten Schritt.
4 Interpretation der einfaktoriellen Varianzanalyse mit Messwiederholung in SPSS (ANOVA)
4.1 Deskriptive Statistiken
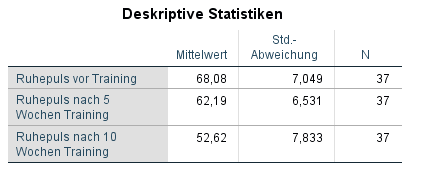
Zunächst ist der Blick ganz kurz auf die deskriptiven Statistiken zu richten. Hier sehen wir die Mittelwerte der zu testenden Variable zu jedem Zeitpunkt. Habt ihr hier kaum Unterschiede in den Mittelwerten gibt es wohl auch keinen signifikanten (also systematischen) Unterschied. Im Beispiel sinkt der Ruhepuls kontinuierlich von 68,08 auf 62,19 (nach 5 Wochen Training) und schließlich 52,62 (nach 10 Wochen Training). Hier könnte es also durchaus einen systematischen Unterschied geben – was für die positive Wirkung des Trainings sprechen würde.
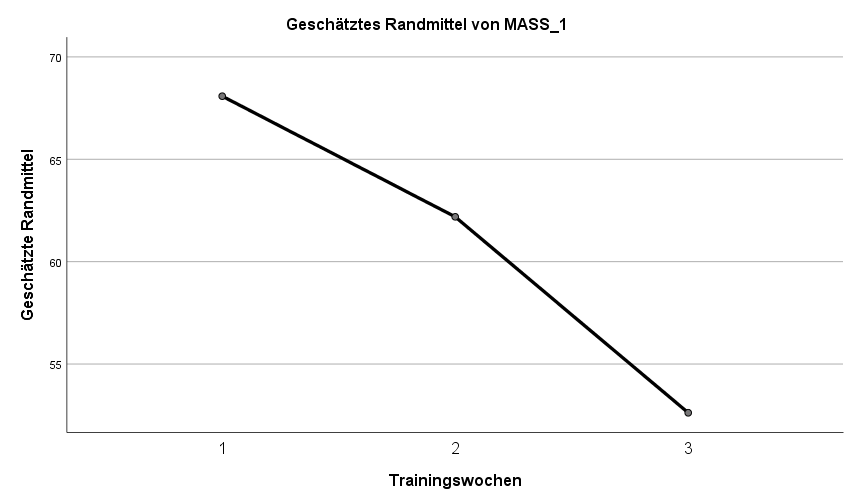
Ganz am Ende des SPSS-Outputs findet sich auch ein Profildiagramm mit den Gschätzten Randmitteln, also den in der Tabelle dargestellten Mittelwerten. Dieses Diagramm zeigt den Abwärtstrend auch recht gut.
4.2 Mauchly-Test auf Sphärizität
Als nächstes ist es notwendig die Sphärizität zu prüfen. Sphärizität ist ungefähre Gleichheit der Varianzen der Differenzen zwischen Zeitpunkten. Anders ausgedrückt: Der Unterschiedsbetrag zwischen t0 und t5 hat eine Varianz, die ungefähr ähnlich groß sein sollte, wie der die Varianz des Unterschiedes zwischen t5 und t10 sowie zwischen t0 und t10. Somit ist auch klar, dass mindestens 3 Zeitpunkte notwendig sind, um überhaupt Sphärizität als Voraussetzung prüfen zu müssen.
Der Mauchly-Test wird hierfür verwendet:

Hier geht es uns eigentlich nur darum zu schauen, ob in der Spalte “Sig.” ein Wert unter 0,05 steht. Bei großen Stichproben sollte man allerdings 0,01 oder sogar 0,001 als Grenze setzen. Ist der p-Wert unter der Alphagrenze, wird die Nullhypothese von Sphärizität verworfen.
Liegt keine Sphärizität vor, müssen wir bei der kommenden Auswertung eine Korrektur vornehmen.
Ein wichtiger Hinweis zum Mauchly’s-Test: bei kleinen Stichproben wird eine Verletzung von Sphärizität häufig nicht erkannt. Bei großen Stichproben sind nur sehr kleine Abweichungen notwendig, um Sphärizität zu verletzen (Vgl. Lantz (2013), weswegen häufig bei großen Stichproben Alpha abgesenkt wird (s.o.). Da dies alles sehr viel Ermessen bietet, ist hier also Vorsicht geboten (vgl. Field (2018), S. 656.
Um dem beschrieben Problem aus dem Weg zu gehen, empfiehlt Field (2018), S. 656 eine pauschale Korrektur, in Verbindung mit dem Wert bei Greenhouse-Geisser in der Mauchly-Test-Tabelle. Ist der Epsilon-Wert bei Greenhouse-Geisser < 0,75, sollte auch die Greenhouse-Geisser-Korrektur (siehe Tabelle: Test der Innersubjekteffekte) angewandt werden. Entsprechend ist Huynh-Feldt bei einem Epsiolon von 0,75 anzuwenden (Field (2018), S. 658). In meinem Fall ist das Epsiolon bei Greenhouse-Geisser mit 0,906 > 0,75 und somit wird die Huynh-Feldt-Korrektur laut Field empfohlen.
4.3 Test der Innersubjekteffekte
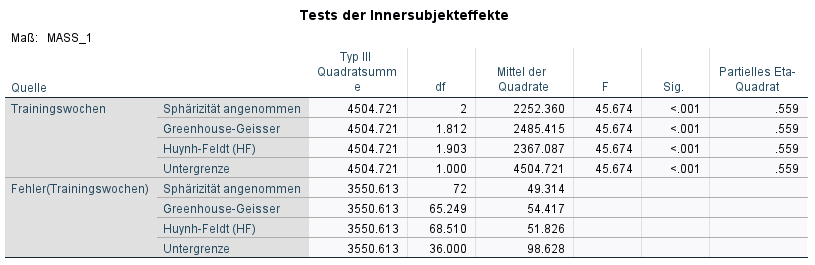
Der Test der Innersubjekteffekte sagt uns, ob wir einen Unterschied der abhängigen Variable im Zeitablauf feststellen konnten. Hier schauen wir in der Spalte “Sig.” nach. Im Beispiel liegt keine Sphärizität vor, weswegen für den Innersubjekteffekt Trainingswochen in der Zeile “Sphärizität angenommen” geschaut werden kann. Folgt man der Empfehlung von Field (2018), würde man bei HF schauen – das Ergebnis ist quasi gleich, mit einem sehr kleinen p-Wert und nur minimal angepassten Freiheitsgraden (df).
Es gibt eine leichte aber kaum ins Gewicht fallende Verletzung in meinem Fall. Das kann bei anderen Stichproben wieder anders aussehen, weswegen eine pauschale Korrektur der sicherste Weg ist. Ist kein Abweichung von Sphärizität gegeben, ist keine Korrektur notwendig und die Ergebnisse identisch, ansonsten gibt es immer mindestens kleine Unterschiede.
Die Signifikanz ist im Beispiel mit p < 0,001 hinreichend klein. Somit wird die Nullhypothese (Gleichheit der Mittelwete) also aufgrund einer hinreichend kleinen Signifikanz verworfen. Somit scheint es wenig wahrscheinlich, dass die Unterschiede zwischen den Zeitpunkten bezüglich des Ruhepulses zufällig zustande gekommen sind. Allerdings ist unklar, zwischen welchen Zeitpunkten ein Unterschied existiert. Hierzu schauen wir in die Post-hoc Tests = paarweise Vergleiche, die wir über die geschätzten Randmittel angefordert hatten.
4.4 Post-hoc Tests
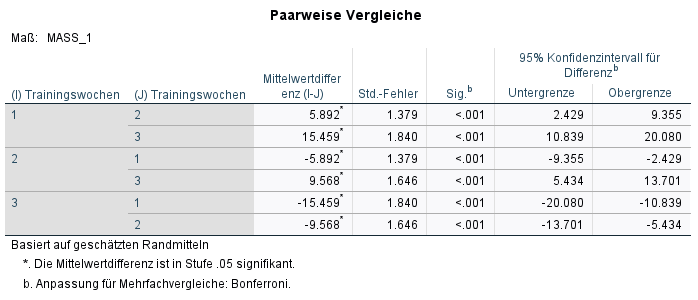
Bei den paarweisen Vergleichen sehen wir nun, ob die Unterschiede zwischen den Messzeitpunkten (Trainingswochen) hinreichend kleine p-Werte aufweisen und damit “überzufällig” sind.
In diesem konstruierten Beispiel ist dies tatsächlich der Fall, da alle paarweisen Vergleiche eine Signifikanz von p < 0,001 aufweisen.
Man kann also schließen:
- Das Training konnte bereits nach 5 Wochen den Ruhepuls bei den Probanden senken (um die Mittlere Differenz von 5,892).
- Außerdem ist der p-Wert für Unterschied zwischen vor dem Training und nach 10 Wochen auch hinreichend klein (p < 0,001), die mittlere Differenz ist 15,459.
- Zusätzlich ist aber auch ein Unterschied zwischen 5 Wochen Training und 10 Wochen Training beobachtbar (mittlere Differenz 9,568, p < 0,001).
Somit kann es aufschlussreich sein, p-Werte über 0,05 auch als Unterschiede/Veränderungen einzuordnen. Wichtig ist hierbei vorherige Evidenz und der Kontext des Untersuchungsdesigns. Zusätzlich kann die Berechnung und das Berichten der Effektstärke des paarweisen Vergleiches vorgenommen werden.
4.5 Ermittlung der Effektstärken
Effektstärke für die ANOVA
Die Effektstärke f wird von SPSS nicht ausgegeben. Die ist, sofern gewünscht, manuell zu berechnen und mit vergleichbaren Studien, fachspezifischen Grenzen oder sofern beides nicht vorhanden, Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 284-287 zu beurteilen. Die Berechnung erfolgt über die Formel mit f als Wurzel aus Eta² geteilt durch 1-Eta².
![Rendered by QuickLaTeX.com \[ f = \sqrt{\frac{\eta^2}{1-\eta^2}} \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-26d88ab04ba79a8988c4e501dc5dbe91_l3.png)
Die Grenzen von Cohen sind 0,1; 0,25 und 0,4 für kleine, mittlere und starke Effekte. Im Beispiel ist das Eta² aus der Tabelle “Test der Innersubjekteffekte” in der Spalte “Partielles Eta-Quadrat” abzulesen. Unabhängig der Korrektur oder nicht ist es immer dasselbe partielle Eta-Quadrat.
Es beträgt in meinem Beispiel 0,559. Wird es in die Formel eingesetzt, ergibt sich ein sehr großes f von 1,126, was einem starken Effekt entspricht.
Effektstärke für post-hoc Tests
Um noch die Effektstärken für die paarweisen Vergleiche aus 4.4 zu ermitteln, werden paarweise t-Tests und die sich hierfür ergebende Effektstärke Cohen’s d bzw. Hedges’ Korrektur von d berechnet.
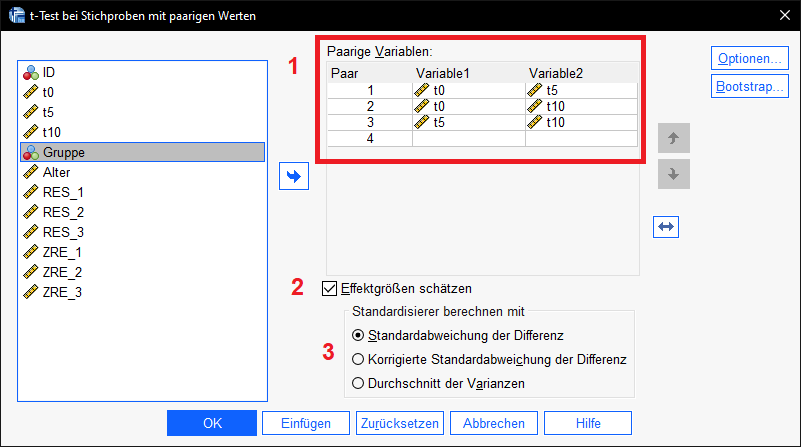
Hierzu geht es über Analysieren > Mittelwerte und Proportionen vergleichen > t-Test bei Stichproben mit paarigen Werten
- (1) Hier sind jeweils bei paarigen Variablen alle paarweisen Vergleiche einzufügen, für die der p-Wert bei den post-Hoc-Tests hinreichend klein war.
- In meinem Beispiel also für alle paarweisen Vergleiche: t0-t5, t0-t10 sowie t5-t10.
- (2)Der Haken bei Effektgrößen schätzen ist standardmäig gesetzt und muss es auch bleiben (ab SPSS 27 verfügbar).
- (3)Die Auswahl des Standardisierers ist eine knifflige Entscheidung, weil die Korrelation der Messwerte zu den Zeitpunkten zu einer mehr oder weniger großen Korrektur führt.
- Hier empfehle ich Grissom, Kim (2012), S. 87-88 zu folgen und (nacheinander) sowohl Standardabweichung der Differenz als auch Korrigierte Standardbabweichung der Differenz anzufordern. Eine höhere Korrelation der Messwerte zwischen den Zeitpunkten sorgt für eine größere Korrektur von Cohen’s d und Hedges’ Korrektur von d. Da in anderen Studien lediglich häufig Cohen’s d berichtet wird, nicht aber, welcher Standardisierer verwendet wurde, kommt es mitunter zu uneinheitlichen Effektstärken.
- Bei der Einordnung der Effektstärken sollte sich – erneut – idealerweise auf ähnliche Studien bezogen werden. Allerdings ist zu beachten, dass von den Autoren mitunter nicht angegeben wurde, welcher Standardisierer verwendet wurde und ein direkter Vergleich nur schwer möglich ist. Normalerweise wird die Standardabweichung der Mittelwertdifferenz verwendet, was in meinem Fall die obere Tabelle “Effektgrößen bei Stichproben mit paarigen Werten” ist.
- Gleiches gilt für fachspezifische Grenzen, die ebenfalls nur sinnvoll einsetzbar sind, wenn klar ist, welcher Standardisierer bei der Effektstärke Cohen’s d verwendet wurde. Auch hier wird normalerweise die Standardabweichung der Mittelwertdifferenz verwendet.
- Schließlich gibt es noch die Möglichkeit, die Grenzen für die Sozial- und Verhaltenswissenschaften (Cohen (1992), S. 157) heranzuziehen, sofern keine der beiden vorgenannten Möglichkeiten der Einordnung existieren. Sie sind 0,2; 0,5 und 0,8 für kleine, mittlere und große Effekte.
- In meinem Beispiel wären die Unterschiede t0-t10 sowie t5-t10 groß sowie t0-t5 mittel – nach Cohen (1992) und wenn der Standardisierer die Standardabweichung der Mittelwertdifferenz ist.
- Ist der Standardisierer die (um die Korrelation der Messwerte) korrigierte Standardabweichung der Differenz, finden die Grenzen nach Cohen (1992) keine Anwendung, da sie nur für die Standardabweichung der Mittelwertdifferenz festgelegt wurden.
- Blanca Mena, M. J., Alarcón Postigo, R., Arnau Gras, J., Bono Cabré, R., & Bendayan, R. (2017). Non-normal data: Is ANOVA still a valid option?. Psicothema, 2017, vol. 29, num. 4, p. 552-557.
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Hillsdale, N.J: L. Erlbaum Associates.
- Cohen, J. (1992). Quantitative methods in psychology: A power primer. Psychol. Bull., 112, 155-159.
- Field, A. (2018), Discovering Statistis using IBM SPSS Statisitics, SAGE
- Grissom, R. J., & Kim, J. J. (2012). Effect sizes for research: Univariate and multivariate applications. Routledge.
- Lantz, B. (2013). The large sample size fallacy. Scandinavian journal of caring sciences, 27(2), 487-492.
- Wasserstein, R. L., & Lazar, N. A. (2016). The ASA statement on p-values: context, process, and purpose. The American Statistician, 70(2), 129-133.
![]()
Cohen’s d teilt die Mittelwertdifferenz durch einen Standardisierer. Dieser kann entweder (1) die Standardabweichung der Mittelwertdifferenzen sein oder (2) die korrigierte Standardabweichung der Mittelwertdifferenzen. Die Möglichkeit den (3) Durchschnitt der Varianzen zu bilden ist nicht zu empfehlen.
Es gibt keine klare Empfehlung, ob für den Standardisierer (1) oder (2) zu wählen ist. Deswegen sollte im Zweifel Cohen’s d mit beiden Standardisierern berechnet und berichtet werden.
 Im Ergebnis erhalte ich einige Tabellen für die paarigen t-Tests, benötige aber jeweils nur die Tabelle “Effektgrößen bei Stichproben mit paarigen Werten”
Im Ergebnis erhalte ich einige Tabellen für die paarigen t-Tests, benötige aber jeweils nur die Tabelle “Effektgrößen bei Stichproben mit paarigen Werten”
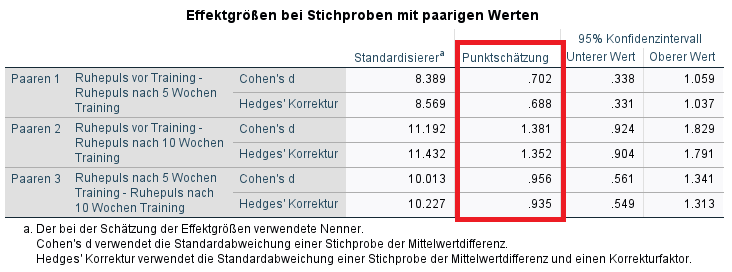
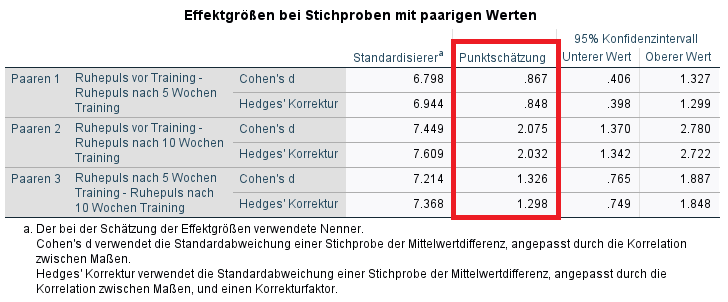
Hier ist deutlich erkennbar, dass z.T. erhebliche Unterschiede zwischen den beiden Berechnungen – je nach Standardisierer – bestehen. Speziell der Unterschied zwischen vor dem Training und nach 10 Wochen (t0-t10) schwankt zwischen d = 1,38 und d = 2,08.
5 Reporting
Fachspezifische Anforderungen sind zu beachten! Hier ein Best-practice-Beispiel.Zunächst wird die ANOVA berichtet. Dazu braucht es lediglich den F-Wert, die Freiheitsgrade und den p-Wert sowie die Effektstärke der ANOVA selbst. Anschließend werden paarweise Vergleiche mit hinreichend kleinen p-Werten berichtet und eingeordnet.
Am Beispiel:
Die ANOVA zeigte einen Effekt des Trainingsplans mit F (2,72) = 45.674; p < 0.001; f = 1.13 / Eta² = 0.559. Die paarweisen Vergleiche zeigten jeweils Signifikanzen von p < 0.001 zwischen t0-t5, t0-t10 sowie t5-t10. Die Effektgröße Cohen's d mit Standardabweichung der Mittelwertdifferenzen als Standardisierer betrug d = 0.70 für t0-t5, d= 1.38 für t0-t10 sowie d = 0.96 für t5-t10. Die so berechneten Effekte könnten nach Cohen (1992) als mittel (t0-t5) sowie groß (t0-t10 und t5-t10) eingeordnet werden.
Cohen’s d mit dem Standardisierer der (um die Korrelation der Messwerte) korrigierten Standardabweichung der Differenz betrug d d = 0.87 für t0-t5, d = 2.08 für t0-t10 sowie d = 1.33 für t5-t10. Eine Einordnung nach Cohen (1992) ist nicht möglich, da die Grenzen sich auf die Standardabweichung der Mittelwertdifferenzen als Standardisierer beziehen.
6 Videotutorial
7 Literatur


