Mediation in R

1 Ziel der Mediation in R

Eine Mediation beschreibt eine Wirkung einer unabhängigen Variable (X) auf eine abhängige Variable (Y) über den Zwischenschritt einer Mediatorvariable (M).
Man kann also getrost von einer Kette sprechen: unabhängige Variable > Mediator > abhängige Variable.

Neben der hier gezeigten Vorgehenswese in R, habe ich noch einen Artikel zur Mediation in SPSS.

Ein Beispiel wäre ein mathematischer Score und wie er auf einen wissenschaftlichen Score wirkt – mediiert durch einen Schreibscore (entnommen aus dem hsb2-Datensatz, siehe unten).
Grafisch sieht eine einfache Mediation ohne weitere unabhängige Variablen wie folgt aus:

 

2 Voraussetzungen der Mediation

Die wichtigsten Voraussetzungen sind, analog zur multiplen linearen Regression:  

• linearer Zusammenhang zwischen x-Variablen und y-Variable
• metrisch skalierte y-Variable (mitunter ist auch ordinal vertretbar – da gibt es große Diskussionen zu :-D)
• keine Multikollinearität – Korrelation der x-Variablen sollte nicht zu hoch sein
• normalverteilte Fehlerterme – Achtung beim analytischen Testen mit Kolmogorov-Smirnov und Shapiro-Wilk-Test
• Homoskedastizität – homogen streuende Varianzen des Fehlerterms
• keine Autokorrelation – Unabhängigkeit der Fehlerterme (Vorsicht bei Durbin-Watson-Test!)
• Kontrolle für einflussreiche Fälle bzw. “Ausreißer”

 

3 Prinzip der Mediation in R

Eine Mediation kann nicht in einem Modell gerechnet werden. Vielmehr ist für jede abhängige Variable, ein separates Modell zu rechnen. Im einfachsten Fall sind dies 2 Modelle, zum einen ist M die abhängige Variable, zum anderen Y.
Modell 1 ist im Beispiel die Wirkung von X auf M. Modell 2 rechnet die gleichzeitige Wirkung von X auf Y und M auf Y.

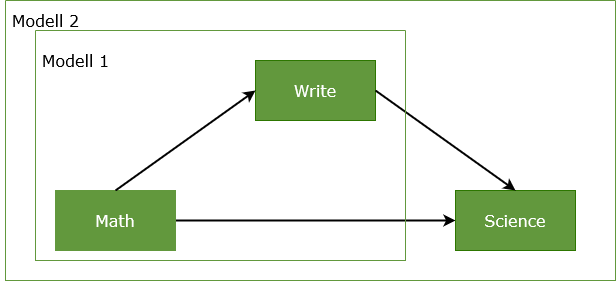
Anders ausgedrückt, prüft man zunächst in Modell 1, ob der Pfad a signifikant ist (X>M) und dann in Modell 2, ob die Pfade b und c signifikant sind (M>Y sowie X>Y):

 

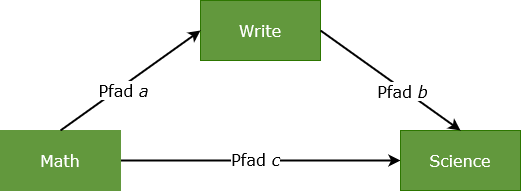
4 Durchführung der Mediation in R

Zunächst lade ich den oben schon erwähnten Beispieldatensatz “hsb2”:

install.packages("openintro")
library(openintro)
data(hsb2)
force(hsb2)

Im Anschluss rechne ich die einzelnen Modelle

 

5 Ergebnis der Mediation in R

5.1 Direkter Effekt von X auf M (Pfad a)

Hierzu wird die lm()-Funktion verwendet und die Ergebnisse in “pfad_a” gespeichert:

pfad_a<-lm(write~math,hsb2)
summary(pfad_a)

Die Ergebnisse (wichtiges in fett) sind wie folgt:

Call:
lm(formula = write ~ math, data = hsb2)

Residuals:
     Min       1Q   Median       3Q      Max 
-24.4956  -4.5277   0.3797   5.3785  16.4997 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 19.88724    3.02411   6.576  4.2e-10 ***
math         0.62471    0.05656  11.045  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.475 on 198 degrees of freedom
Multiple R-squared:  0.3812,	Adjusted R-squared:  0.3781 
F-statistic:   122 on 1 and 198 DF,  p-value: < 2.2e-16

• Das Modell ist signifikant (F(1,198) = 122, p < 0,001), leistet also einen signifikanten Erklärungsbeitrag. Ist p > 0,05 wirkt X nicht auf M. Das zweite Modell ist dann noch zu rechnen.
• Die unabhängige Variable "math" wirkt signifikant (p < 0,001) auf die abhängige Variable "write".
• Der Koeffizient ist mit 0,624 > 0.
  Eine Zunahme von "math" um eine Einheit wirkt positiv (um 0,624 Einheiten) auf "write".
• Der Intercept wird trotz Signifikanz ignoriert.
• Die Varianzaufklärung der abhängigen Variable "write" beträgt 38,12% (Multiple R-squared).

 

5.2 Direkter Effekt von X auf Y und Effekt von M auf Y (Pfad c und b)

pfad_b_c<-lm(science~math+write, hsb2)
summary(pfad_b_c)

Die Ergebnisse (wichtiges in fett) sind wie folgt:

Call:
lm(formula = science ~ math + write, data = hsb2)

Residuals:
     Min       1Q   Median       3Q      Max 
-20.8827  -4.8924  -0.2717   4.0738  23.6972 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 10.68138    3.29339   3.243  0.00139 ** 
math         0.47570    0.07094   6.706 2.07e-10 ***
write        0.30555    0.07012   4.358 2.11e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.375 on 197 degrees of freedom
Multiple R-squared:  0.4508,	Adjusted R-squared:  0.4452 
F-statistic: 80.84 on 2 and 197 DF,  p-value: < 2.2e-16

• Auch dieses Modell ist signifikant (F(2,197) = 80,84, p < 0,001). Ist p > 0,05, muss an dieser Stelle abgebrochen werden, da X und M zusammen keinen signifikanten Erklärungsbeitrag bzgl. Y leisten.
• Die unabhängige Variable "math" wirkt signifikant (p < 0,001) auf die abhängige Variable "science".
• Der Koeffizient ist mit 0,476 > 0.
  Eine Zunahme von "math" um eine Einheit wirkt positiv (0,476 Einheiten) auf "science".
• Die unabhängige Variable "write" (Mediator) wirkt signifikant (p < 0,001) auf die abhängige Variable "science".
• Der Koeffizient ist mit 0,306 > 0.
  Eine Zunahme von "math" um eine Einheit wirkt positiv (0,306 Einheiten) auf "science".
• Der Intercept wird trotz Signifikanz ignoriert.
• Die Varianzaufklärung der abhängigen Variable "science" beträgt 45,08% (Multiple R-squared).

 

5.3 Untersuchung des Mediationseffektes

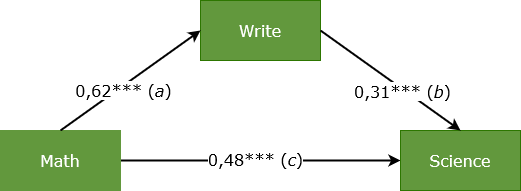
• Offensichtlich sind Pfad a und Pfad b jeweils signifikant. "math" wirkt auf "write" und "write" wirkt auf "science".
• Eine Mediation scheint also im vorliegenden Datensatz von "math" auf "science" über den Mediator "write" zu existieren.
• Zusätzlich ist auch Pfad c signifikant, was eine direkte Wirkung von "math" auf "science" bedeutet.

Im nächsten Schritt ist zu prüfen, welcher Anteil des Effektes von "math" auf "science" über den Mediator, also Pfad a und b läuft.
Hierzu wird das mediation-Paket benötigt. Es kann zwar auch händisch berechnet werden, hiermit ist es aber bequemer und übersichtlicher:

install.packages("mediation")
library(mediation)

Anschließend werden in die mediate()-Funktion die beiden obigen Modellergebnisse hineingegeben und mit treat = "math" die X-Variable und mit mediator = "write" die Mediatorvariable definiert.
Mit boot = TRUE werden die Konfidenzintervalle mithilfe des Bootstrappings berechnet.

results <- mediate(pfad_a, pfad_b_c, 
                   treat = "math", mediator = "write", 
                   boot = TRUE)
summary(results)

Das Ergebnis ist nun folgendes:

Causal Mediation Analysis 

Nonparametric Bootstrap Confidence Intervals with the Percentile Method

               Estimate 95% CI Lower 95% CI Upper p-value    
ACME             0.1909       0.0963         0.30  <2e-16 ***
ADE              0.4757       0.3206         0.63  <2e-16 ***
Total Effect     0.6666       0.5548         0.77  <2e-16 ***
Prop. Mediated   0.2864       0.1407         0.47  <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Sample Size Used: 200 


Simulations: 1000 

Zum indirekten Effekt:

• ACME ist der average causal mediation effect. Das ist der indirekte Effekt (Pfad a und b) von "math" über "write" auf "science".
• Er ist positiv mit 0,1909. Er ergibt sich aus dem Produkt der Koeffizienten von "math" auf "write" (a) und "write" auf "science" (b).
• ACME = a*b = 0,62471*0,30555 = 0,1909.
• Der indirekte Effekt ist signifikant (p < 0,001).
• Es liegt eine Mediation des Effektes von "math" auf "science" durch "write" vor.

Zum direkten Effekt

• ADE ist der average direct effect und ist der Koeffizient von "math" (Pfad c) in Modell 2.
• Unter Kontrolle für den Effekt von "write" auf "science" ist dieser ebenfalls signifikant (p < 0,001).

Gesamteffekt ("Totaler Effekt")

• Der Total Effect ergibt sich aus Addition von indirektem und direktem Effekt, also ACME + ADE.
• ACME + ADE = (a*b)+c = 0,62471*0,30555 + 0,4757 = 0,1909 + 0,4757 = 0,6666 (Abbildung enthält gerundete Werte)
• Steigt also "math" um eine Einheit, so steigt "science" in Summe um 0,6666 Einheiten.
• 0,1909 Einheiten ergeben sich aus dem indirekten Effekt, 0,4757 Einheiten aus dem direkten Effekt.

Stärke der Mediation

• Prop. Mediated gibt an, wie hoch der prozentuale Anteil von ACME am Total Effect ist.
• Einfacher gesagt: wie viel Prozent des Effektes geschieht über die Mediation.
• Im Beispiel ist dies 0,1909 / 0,666 = 0,2864.
• 28,64 % des totalen Effektes von "math" auf "science" wird also über den Mediator "write" erzielt.

 

6 Einordnung der Mediation

Schließlich ist die Mediation noch einzuordnen. Hierfür ist Zaho, Lynch (2010) auf S. 201 anwendbar.

Das Flussdiagramms wird von oben nach unten durchgearbeitet und die oben eingeführten und berechneten Pfade verwendet.
Aus didaktischen Gründen arbeite ich die 5 möglichen Ausgänge ab und deren unterschiedliche Pfade.

• Complementary Mediation: Die Pfade a*b sowie c sind signifikant. Zudem ist das Produkt aus a*b*c positiv. Das ist ein Hinweis auf den unterstellten Mediator, allerdings ist es auch wahrscheinlich, dass ein weiterer Mediator existiert. Das liegt daran, dass der signifikante direkte Effekt möglicherweise noch Teile eines weiteren Mediators enthält. Das theoretische Framework sollte hier hinterfragt und evtl. überarbeitet werden.
• Competitive Mediation: Die Pfade a*b sowie c sind signifikant. Zudem ist das Produkt aus a*b*c negativ, die Effekte sind also gegenläufig. Das ist ein Hinweis auf den unterstellten Mediator, allerdings ist es auch wahrscheinlich, dass ein weiterer Mediator existiert. Das liegt möglicherweise daran, dass der signifikante direkte Effekt noch Teile eines weiteren Mediators enthält. Das theoretische Framework sollte auch hier hinterfragt und evtl. überarbeitet werden.
• Indirect-only Mediation: Die Pfade a*b aber nicht c sind signifikant. Das ist sozusagen der Idealfall, weil die emprisichen Ergebnisse mit der Theorie bzw. dem daraus abgeleiteten Modell übereinstimmen. Die Existenz eines weiteren Mediators ist unwahrscheinlich. Das liegt möglicherweise daran, dass der direkte Effekt nach Aufnahme des Mediators nicht (mehr) signifikant ist.
• Direct-only (Non-Mediation): Die Pfade a*b sind nicht signifikant, der Pfad c ist jedoch signifikant. Der unterstellte Mediator konnte nicht empirisch beobachtet werden, jedoch ein direkter Effekt. Das kann ein Hinweis für ein mangelndes theoretisches Framwork sein. Mitunter existiert ein anderer Mediator, aber nicht zwingend.
• No-Effect (Non-Mediation):Die Pfade a*b sowie der Pfad c sind nicht signifikant. Weder der unterstellte Mediator noch der direkte Effekt konnte empirisch beobachtet werden. Das ist ein Hinweis auf einen möglicherweise nicht existenten Mediator, aber Achtung, wie oben bereits ausgeführt, kann der Fall auftreten, dass eine "competitive mediation" mit einem anderen Mediator existert. Das theoretische Framework ist hier in jedem Fall zu hinterfragen.

Abschließende Hinweise:

• Im Beispiel liegt eine komplementäre Mediation vor. Das ist ein Hinweis auf einen weiteren Mediator. Tatsächlich existert im hsb2-Daten noch die Variable "read" (der Lesescore), welche hinzugezogen werden und eine parallele Mediation gerechnet werden kann.
• Sofern Effekte in der Realität existieren, sie also verschieden von 0 sind, ist die Stichprobengröße und damit die statistische Power ein grundlegender Faktor beim Erkennen jener Effekte. Je kleiner Effekte sind, desto größer muss eine Stichprobe sein, um diesen Effekt erkennen zu können (Vgl. Cohen (1988), S. 10-11.
• Die Größe des p-Wertes sagt nichts über die Größe oder Bedeutsamkeit eines Effektes aus (vgl. Wasserstein, Lazar (2017), S. 132).
• Diese Tatsache zeige ich in diesem Blogbeitrag.
  Im Nachhinein kann aber NICHT mit einer sog. Post hoc Poweranalyse argumentiert werden, dass Effekte nicht erkannt wurden, weil die Power zu niedrig war (Hoenig, Heisey (2001), S. 20: “Observed power can never fulfill the goals of its advocates because the observed significance level of a test
  (“p value”) also determines the observed power; for any test the observed power is a 1:1 function of the p value.”).
• In jeder Regression sind weitere Kontrollvariablen ("Kovariate") zu berücksichtigen. Hierzu gehören meist soziodemokartische Faktoren oder bereits in der Literatur nachgewiesene Einflussfaktoren. Deren Nichtberücksichtigung im Modell würde bedeuten, dass man deren möglichen (oder bereits nachgewiesenen) Einfluss ignoriert oder ihn beliebig an- und abschalten kann.
  Einfach ausgedrückt: das Diabetesrisiko steigt bei Kindern und Jugendlichen. Bei übergewichtigen ist es jedoch 4 mal höher (Vgl. Abbasi et al (2017)) - das Ignorieren des Gewichts wäre also fahrlässig.

 

7 Videotutorial

Dieses Video auf YouTube ansehen.

 

8 Literatur

• Abbasi, A., Juszczyk, D., van Jaarsveld, C. H., & Gulliford, M. C. (2017). Body mass index and incident type 1 and type 2 diabetes in children and young adults: a retrospective cohort study. Journal of the Endocrine Society, 1(5), 524-537.
• Baron, R. M., & Kenny, D. A. (1986). The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of personality and social psychology, 51(6), 1173.
• Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.). Routledge.
• Hayes A. F. (2022). Introduction to mediation moderation and conditional process analysis : a regression-based approach (Third). Guilford Press.
• Hoenig, J. M., & Heisey, D. M. (2001). The abuse of power: the pervasive fallacy of power calculations for data analysis. The American Statistician, 55(1), 19-24.
• Wasserstein, R. L., & Lazar, N. A. (2016). The ASA statement on p-values: context, process, and purpose. The American Statistician, 70(2), 129-133.
• Zhao, X., Lynch Jr, J. G., & Chen, Q. (2010). Reconsidering Baron and Kenny: Myths and truths about mediation analysis. Journal of consumer research, 37(2), 197-206.

 

9 Datensatz

Der Datensatz kann direkt in R geladen werden:

install.packages("openintro")
library(openintro)
data(hsb2)
force(hsb2)