Der Kolmogorov-Smirnov-Test in R hilft bei der Beurteilung, ob eine Variable, wahlweise auch Residuen, normalverteilt sind. Allerdings sollte man bei der Beurteilung vorsichtig sein, was auch für den Shapiro-Wilk-Test auf Normalverteilung gilt.
Inhaltsverzeichnis
1 Nullhypothese des Kolmogorov-Smirnov-Tests
Der Kolmogorov-Smirnov-Test prüft die zu testende Variable auf Normalverteilung.
Demzufolge lautet die Nullhypothese des Kolmogorov-Smirnov-Tests:
Es liegt Normalverteilung vor.
2 Rechnen des Kolmogorov-Smirnov-Tests in R
Der Kolmogorov-Smirnov-Test wird in R über die ks.test()-Funktion berechnet.
Neben der zu testenden Variable benötigt man 3 Argumente, die für die Berechnung mitgegeben werden müssen, um zu prüfen, wie stark die zu testende Variable von einer Normalverteilung abweicht:
- Zunächst braucht es in Anführungszeichen das Argument “pnorm”.
- Daran schließt sich der Mittelwert der Variable an
- Schließlich muss die Standardabweichung der zu testenden Variable angegeben werden.
Mittelwert und Standardabweichung werden für die Testvariable (df$Gewicht) einfach über die mean()-Funktion und die sd()-Funktion berechnet.
Für meine zu testende Variable “Gewicht” aus dem Data Frame “df” sieht der Kolmogorov-Smirnov-Test wie folgt aus:
ks.test(df$Gewicht, "pnorm", mean=mean(df$Gewicht), sd=sd(df$Gewicht))
Im Ergebnis erhält man eine Teststatistik D sowie den p-Wert:
Asymptotic one-sample Kolmogorov-Smirnov test
data: df$Gewicht
D = 0.1908, p-value = 0.04879
alternative hypothesis: two-sided
3 Beurteilen des Kolmogorov-Smirnov-Tests in R
Der p-Wert dient mir zum Prüfen der Nullhypothese. Liegt der p-Wert unter dem vorher definierten Alphaniveau (zumeist 5% = 0,05), wird die Nullhypothese verworfen. Wir erinnern uns, dass die Nullhypothese beim Kolmogorov-Smirnov-Test gleichbedeutend mit Normalverteilung ist.
Folglich führt ein Verwerfen der Nullhypothese dazu, dass man keine Normalverteilung attestieren kann.
Dies trifft auf das oben gerechnete Beispiel zu. Da p = 0,0488 < 0,05 muss die Nullhypothese von Normalverteilung verworfen werden.
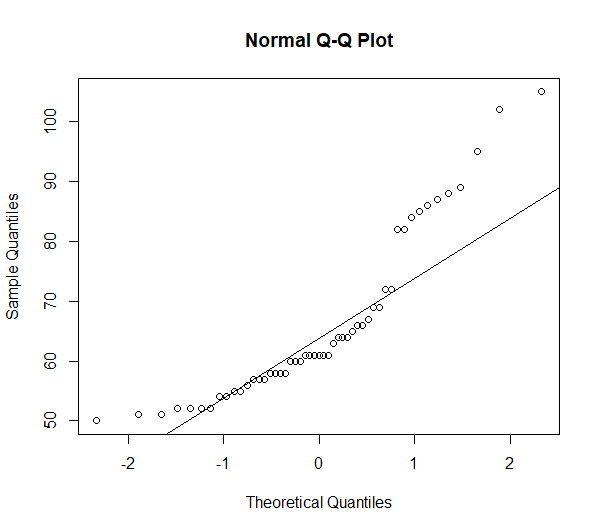
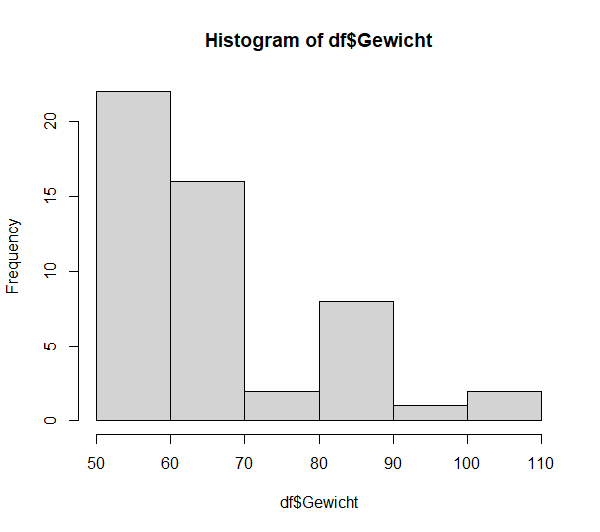
Beim Betrachten des Q-Q-Plots (näheres zur Lesart) und Histogramms wird schnell klar, dass dies korrekt scheint. Die Abweichungen von einer Normalverteilung sind zu groß.
hist(df$Gewicht)
qqnorm(df$Gewicht)
qqline(df$Gewicht)
4 Zweites Beispiel
ks.test(df2$x, "pnorm", mean=mean(df2$x), sd=sd(df2$x))
Im Ergebnis erhält man:
Asymptotic one-sample Kolmogorov-Smirnov test
data: df2$x
D = 0.0079442, p-value = 0.9105
alternative hypothesis: two-sided
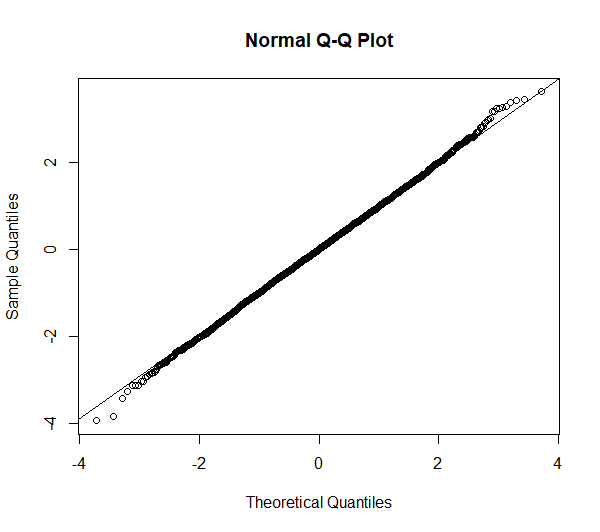
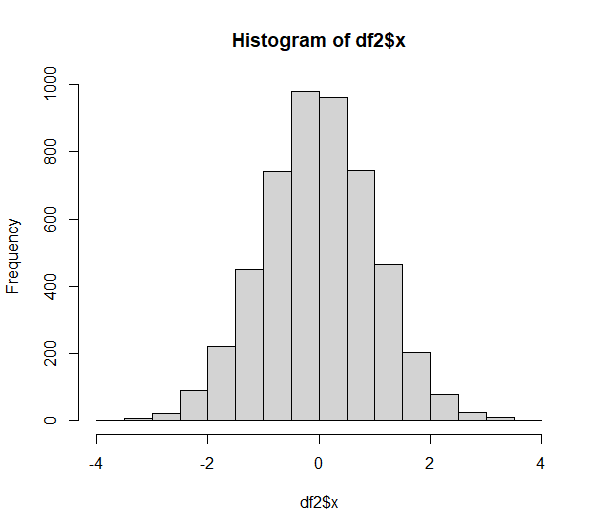
Die Nullhypothese wird bei dieser (im Vorfeld absichtlich als normalverteilte Variable erstellte) Verteilung mit 5000 Beobachtungen mit einem p-Wert von p = 0,9105 nicht verworfen. Die Testvariable ist normalverteilt, was sich beim Blick auf Q-Q-Plot und Histogramm bekräftigt:
5 Vorsicht beim Kolmogorov-Smirnov-Test!
Ein letztes Beispiel dient dazu, vor der alleinigen Verwendung des Ergebnisses des Kolmogorov-Smirnov-Tests zu warnen.
Eine Variable, analog zu oben, mit 5000 Beobachtungen, allerdings mit ein paar Beobachtungen an den Verteilungsrändern um 3 bzw. -3 und 4 bzw. -4.
Asymptotic one-sample Kolmogorov-Smirnov test
data: df2$x
D = 0.019354, p-value = 0.04723
alternative hypothesis: two-sided
Das Ergebnis ist hier eine Verwerfung der Nullhypothese von Normalverteilung. Allerdings stellt sich die Frage, ob das gerechtfertigt ist, wenn Q-Q-Plot und Histogramm betrachtet werden:
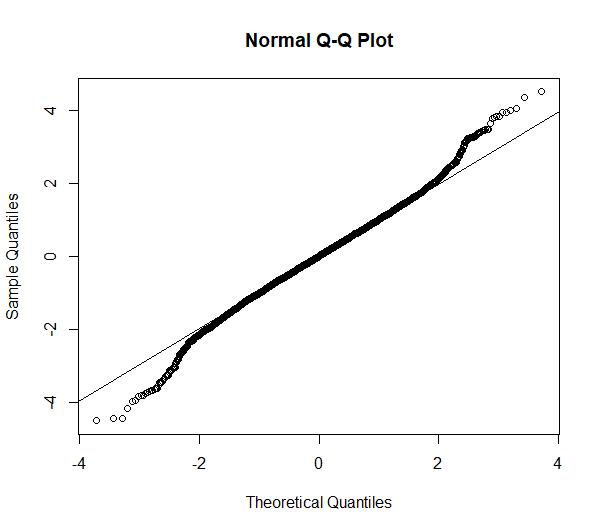
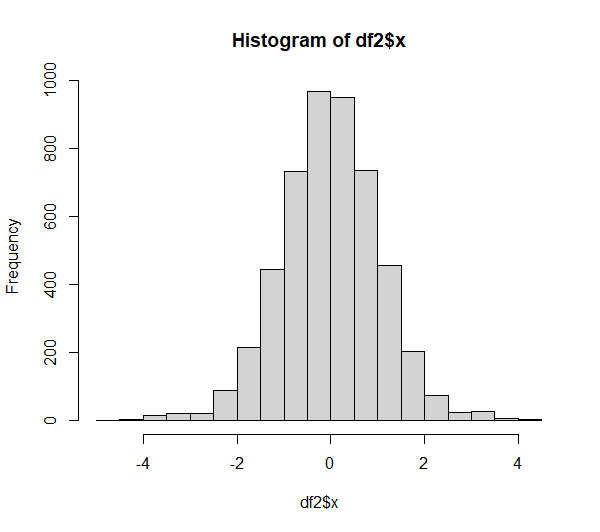
Hier kann geschlossen werden, dass, obwohl der Kolmogorov-Smirnov-Test hier keine Normalverteilung attestiert (beim Alphaniveau von 5%), grafisch betrachtet aber kaum Grund zum Zweifeln an Normalverteilung besteht.
Die im Q-Q-Plot sichtbaren Abweichungen an den Enden der Verteilung sind unter praktischen Gesichtspunkten im wahrsten Sinne des Wortes normal. In solchen Fällen ist die typische Anforderung parametrischer Tests an z.B. normalverteilte Residuen erfüllt, da eine “in etwa Normalverteilung” ausreicht – obwohl der Kolmogorov-Smirnov-Test keine Normalverteilung attestiert.
- Der Grund für dieses Testergebnis ist die höhere Stichprobengröße.
- Diese führt zu einer höheren Power (= Teststärke) des Kolmogorov-Smirnov-Tests.
- Eine höhere Power bedeutet, dass kleinere Abweichungen wahrscheinlicher entdeckt werden.
- Kleine Abweichungen führen bei großen Stichproben also letztlich zur Verwerfung der Nullhypothese (von Normalverteilung)
- Zusätzlich fehlt dem Kolmogorov-Smirnov-Test bei kleinen Stichproben die Power, tatsächlich relevante Abweichungen von Normalverteilung aufzudecken (Aldor-Noiman (2013)).
Im Artikel “The large sample size fallacy” von Lantz (2013) wird das Phänomen sinkender p-Werte bei steigenden Stichprobengrößen ausführlich beschrieben.
Zusammengefasst aus dem Abstract: “The results of studies based on large samples are often characterized by extreme statistical significance despite small or even trivial effect sizes. Interpreting such results as significant in practice without further analysis is referred to as the large sample size fallacy in this article.“
5 Videotutorial
6 Literatur
- Lantz, B. (2013). The large sample size fallacy. Scandinavian journal of caring sciences, 27(2), 487-492.
- Sivan Aldor-Noiman, Lawrence D. Brown, Andreas Buja, Wolfgang Rolke & Robert A. Stine (2013) The Power to See: A New Graphical Test of Normality, The American Statistician, 67:4, 249-260, DOI: 10.1080/00031305.2013.847865


