Dieser Beitrag zeigt die Durchführung für die zweifaktorielle ANOVA in R und ist stark angelehnt an das Kapitel 12.1 zur mehrfaktoriellen ANOVA in meinem Buch “Statistik mit R – Schnelleinstieg” (Amazon-Affiliatelink). Die Daten sind NICHT identisch, um zusätzlich einen Interaktionseffekt zeigen zu können. Zudem sind die Daten fiktiv.
Inhaltsverzeichnis
1 Ziel der zweifaktoriellen Varianzanalyse (ANOVA)
Die mehrfaktorielle ANOVA testet zwei oder mehr Faktoren, isoliert und interagierend auf Unterschiede hinsichtlich einer Testvariable. Die Nullhypothese lautet, dass keine Mittelwertunterschiede (hinsichtlich der Testvariable) existieren. Demzufolge lautet die Alternativhypothese, dass zwischen den Gruppen Unterschiede existieren. Es ist das Ziel, die Nullhypothese zu verwerfen und die Alternativhypothese anzunehmen. Es gibt auch ein Tutorial zur Durchführung in SPSS.
2 Voraussetzungen der zweifaktoriellen Varianzanalyse (ANOVA)
Die wichtigsten Voraussetzungen der ANOVA sind:
- mindestens zwei Faktoren
- metrisch skalierte y-Variable
- normalverteilte Fehlerterme
- Varianzhomogenität
Bei Nichterfüllung der Voraussetzungen sollte auf die nichtparametrische Alternative zurückgegriffen werden, die auf “Aligned Rank Transform” aufbaut und im “ARTool”-Paket implementiert ist.
3 Das Beispiel und Forschungsfrage(n)
Das Beispiel beinhaltet fiktive Einkommensdaten für Frauen und Männer. Gleichzeitig ist die Erfahrungsstufe erfasst.
Es gibt also zwei Faktoren:
- Geschlecht
- Erfahrungsstufe
Die Frage ist, ob das Geschlecht, die Erfahrungsstufe oder beides in Kombination auf das Gehalt wirkt. Insbesondere der Geschlechterunterschied wird unter dem Stichwort “gender pay gap” zusammengefasst (vgl. Hoff (2021)).
Evidenz für das Alter und das gender pay gap in Kombination findet sich z.B. bei Schrenker, Zucco (2020). Ein weiterer der Autoren identifizierter Faktor ist der Wohnort, welcher aus Komplexitätsgründen in diesem Beispiel allerdings nicht mitmodelliert wird.
3 Deskriptive Voranalyse und Voraussetzungsprüfung in R
3.1. Deskriptive Voranalyse
Nach dem Einlesen der Daten kann direkt ein deskriptiver Vergleich gestartet werden, der im Rahmen der ANOVA nicht zwingend notwendig ist, beim Schreiben der Ergebnisse hilft und für einen ersten Eindruck sehr hilfreich ist.
Hierzu nutze ich Pipes mit dem Paket “dplyr”, was ich mit “install.packages” installiere und mit library(dplyr) lade. Ich lasse mir den Mittelwert (mean), die Standardabweichung (sd) und die Anzahl der Beobachtungen pro Gruppe (n) ausgeben.
install.packages("dplyr")
library(dplyr)
data %>%
group_by(Geschlecht, Erfahrung) %>%
summarize(M = mean(Einkommen),
SD = sd(Einkommen),
N = n()) %>%
as.data.frame()
Hier erhält man folgenden Output:
Geschlecht Erfahrung M SD N
1 Frau 1 2444.138 629.6060 29
2 Frau 2 2483.714 720.0167 35
3 Frau 3 3622.692 718.7465 26
4 Frau 4 3843.478 577.4522 23
5 Mann 1 2913.226 793.8698 31
6 Mann 2 3555.714 687.3429 28
7 Mann 3 3863.429 839.1205 35
8 Mann 4 4241.515 820.5491 33
Dies kann zusätzlich mit Boxplots noch grafisch veranschaulicht werden. Am einfachsten mit dem Paket “ggpubr”:
install.packages("ggpubr")
library(ggpubr)
ggboxplot(data, x = "Erfahrung", y = "Einkommen", fill = "Geschlecht")

Hier ist schon folgendes erkennbar: die Mittelwerte unterscheiden sich sowohl a) innerhalb des Geschlechts über die Erfahrung hinweg als auch b) zwischen den Geschlechtern auf denselben Erfahrungsstufen.
Die Fragen, die mit der zweifaktoriellen ANOVA beantworten werden soll: Gibt es Erfahrungsunterschiede, Geschlechterunterschiede, “Kombinationsunterschiede”?
3.2 Normalverteilung prüfen
Hierzu nutze ich ein Q-Q-Plot, welches ich mit der Funktion ggqqplot()-Funktion aus dem “ggpubr”-Paket erstelle. Es ist allerdings notwendig, vorher die Residuen zu ermitteln, da diese abgetragen und geprüft werden müssen.
Diese werden mit der lm()-Funktion berechnet und im Vektor nv gespeichert.
Residuen sind der Unterschied zwischen durch das Modell geschätzten und tatsächlichen y-Werten.
nv <- lm(Einkommen ~ Geschlecht*Erfahrung, data = data)
library(ggpubr)
ggqqplot(residuals(nv))
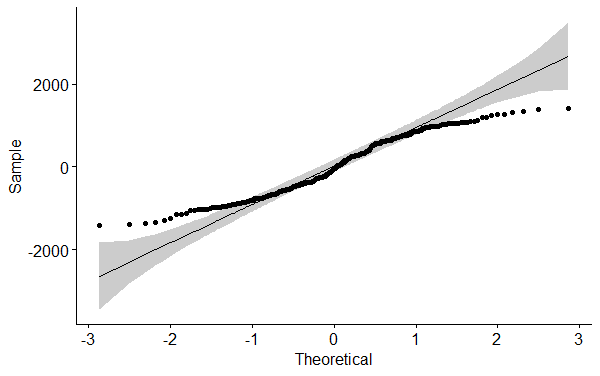
Die Punkte repräsentieren die einzelnen Residuen. Sie liegen bei perfekter Normalverteilung auf der Geraden. Der graue Bereich ist das Konfidenzintervall um die Gerade.
In praktischen Anwendungsfällen existieren naturgemäß Abweichungen, speziell an den Rändern. Oben rechts und unten links liegen die Punkte meist etwas weiter von der Geraden weg. Im Normalfall sind leichte Abweichungen wie in der Abbildung in Ordnung, da die ANOVA relativ robuste Ergebnisse liefert (vgl. Blanca et al. (2017)).
3.3 Varianzhomogenität prüfen
Es gibt zwei Möglichkeiten. Die erste ist NICHT zu empfehlen und wird hier nur der Vollständigkeit wegen gezeigt.
1. Möglichkeit
In vielen (alten) Publikationen wird der Levene's Test herangezogen, dessen Nullhyopthese von Varianzgleichheit ausgeht:
library(car)
leveneTest(data = data, Einkommen~Geschlecht*Erfahrung)
- Bei kleinen Stichproben fehlt die Power und die Wahrscheinlichkeit eines Fehlers 2. Art steigt.
- Bei großen Stichproben wird der p-Wert automatisch kleiner. Die Chance einen Fehler 1. Art zu begehen steigt.
2. Möglichkeit
Wie auch beim Test auf Normalverteilung, sollte Varianzhomogenität wegen der Erläuterungen von oben grafisch geprüft werden:
plot(nv,1)

Die Linie sollte ohne "Dellen" auskommen, also möglichst gerade in x-Richtung verlaufen. Dies kann hier als erfüllt angesehen werden.
4 Die zweifaktorielle ANOVA in R rechnen und interpretieren
Sind die Voraussetzungen inreichend erfüllt, wird die anova_test()-Funktion des rstatix-Pakets verwendet:
install.packages("rstatix")
library(rstatix)
anova_test(data = data, Einkommen~Geschlecht*Erfahrung, effect.size = "pes")
- Die abhängige Variable kommt zuerst in die Formel.
- Eine Interaktion von zwei Faktoren wird durch * angegeben, also im Beispiel Geschlecht*Erfahrung.
- Sollte keine Interaktion gewünscht sein, wird lediglich + zwischen die Faktoren geschrieben.
- Hinweis: Sollte eine Interaktion definiert werden, werden die Faktoren automatisch auch einzeln mitberechnet.
ANOVA Table (type II tests)
Effect DFn DFd F p p<.05 pes
1 Geschlecht 1 232 33.311 2.50e-08 * 0.126
2 Erfahrung 3 232 42.210 8.34e-22 * 0.353
3 Geschlecht:Erfahrung 3 232 3.725 1.20e-02 * 0.046
Im Output ist eigentlich nur ein Wert wirklich interessant: der in fett hervorgehobene p-Wert.
- Zunächst kann hier beobachtet werden, dass sowohl die Faktoren Geschlecht (p < 0,001) als auch Erfahrung (p < 0,001) einen Einfluss auf die abhängige Variable, das Einkommen, haben.
- Weiterhin zeigt der Interaktionseffekt aus Geschlecht und Erfahrung einen recht kleinen Signifikanzwert mit p = 0,012.
Hinweis: Sollte der Interaktionseffekt einen hinreichend kleinen p-Wert haben (wie im Beispiel) haben, sind die sog. Haupteffekte, also Geschlecht und Erfahrung für sich genommen, NICHT zu interpretieren.
Es wurde gerade festgestellt, dass nicht das isolierte Wirken der beiden Faktoren, sondern deren Zusammenwirken auf die Testvariable einen Einfluss haben.
Umgekehrt können bei einem zu großen p-Wert der Interaktion wiederum die Faktoren einzeln betrachtet werden.
Speziell im Falle eines beobachteten Interaktionseffektes ist es von Interesse, wo genau Unterschiede bestehen, also zwischen welchen Kombinationen von Erfahrung und Geschlecht (siehe 5). Sind nur die Faktoren einzeln signifikant, kann je Faktor eine post-hoc-Analyse gerechnet werden (siehe 4).
5 Post-hoc-Analyse bei nicht signifikanter Interaktion
Dieser Abschnitt ist nur relevant, wenn NUR die Haupteffekte signifikant sind.
In meinem Beispiel ist der Interaktionseffekt signifikant und ich zeige das Vorgehen für die Haupteffekte an dieser Stelle nur exemplarisch.
- Da das Geschlecht im Beispieldatensatz nur zwei Ausprägungen hat, muss und kann hierfür kein Post-hoc-Test gerechnet werden. Zudem war in der deskriptiven Voranalyse ersichtlich, dass Frauen ein niedrigeres Bruttoeinkommen erzielen. Dieser Unterschied kann bereits als signifikant festgehalten werden.
- Die Erfahrung hat allerdings vier Ausprägungen, weshalb hierfür Post-hoc-Tests notwendig sind, um zu sehen, zwischen welchen Erfahrungsstufen signifikante Unterschiede bestehen. Bei mehr als einem signifikanten Hauptfaktor ist im unteren Code entsprechend der Faktor auszutauschen, also z.B. "Geschlecht" statt "Erfahrung".
Im rstatix-Paket kann dafür die pairwise_t_test()-Funktion verwendet werden, die erneut bequem mit Piping (%>%) angesprochen wird. Für Mehrfachvergleiche und damit Alphafehlerkumulierung wird mit der Bonferroni-Methode korrigiert.
# post-hoc-Tests bei signifikanter ANOVA rechnen
data %>%
pairwise_t_test(Einkommen~Erfahrung, pool.sd = TRUE,
p.adjust.method = "bonferroni") %>%
as.data.frame()
Der Output ist folgender:
.y. group1 group2 n1 n2 p p.signif p.adj p.adj.signif
1 Einkommen 1 2 60 63 5.85e-02 ns 3.51e-01 ns
2 Einkommen 1 3 60 61 2.33e-12 **** 1.40e-11 ****
3 Einkommen 2 3 63 61 6.41e-08 **** 3.84e-07 ****
4 Einkommen 1 4 60 56 5.53e-18 **** 3.32e-17 ****
5 Einkommen 2 4 63 56 5.87e-13 **** 3.52e-12 ****
6 Einkommen 3 4 61 56 3.28e-02 * 1.97e-01 ns
Hier ist erkennbar, dass sich das Einkommen für beide Geschlechter zusammengenommen zwischen der Erfahrungsstufe 1 und 3, 2 und 3, 1 und 4 sowie 2 und 4 (p-Werte fett) unterscheidet. Zwischen den Erfahrungsstufen 1 und 2 sowie 3 und 4 gibt es keine hinreichenden Unterschiede.
Für Gruppenvergleiche mit hinreichend kleinem p-Wert können zudem noch Effektstärken berechnet werden. Hierzu kann, da es sich um t-Tests handelt, Cohen's d berechnet werden:
data%>%
cohens_d(Einkommen~Erfahrung)%>%
as.data.frame()
Das führt zu folgendem Output:
.y. group1 group2 effsize n1 n2 magnitude
1 Einkommen 1 2 -0.334 60 63 small
2 Einkommen 1 3 -1.39 60 61 large
3 Einkommen 1 4 -1.85 60 56 large
4 Einkommen 2 3 -0.955 63 61 large
5 Einkommen 2 4 -1.36 63 56 large
6 Einkommen 3 4 -0.411 61 56 small
Nur die Effektstärken für Vergleiche mit hinreichend kleinem p-Wert (hier in fett) sind zu berichten. Zudem werden Effektstärken stets als Betrag (positiv) berichtet.
Die Einordnung erfolgt anhand fachspezifischer Grenzen. Sollten keine existieren, kann Cohen (1992): A Power Primer, S. 157 herangezogen werden. Die Grenzen für kleine, mittlere und große Effekte werden mit 0,2; 0,5 und 0,8 angegeben und werden hier auch in der Spalte "magnitude" direkt angegeben.
Die signifikanten Unterschiede weisen allesamt eine große Effektstärke und damit einen großen Unterschied zwischen den Erfahrungsstufen aus.
6 Post-hoc-Analyse bei signifikanter Interaktion
Wie bereits erwähnt, sind bei einer signifikanten Interaktion die Haupteffekte nicht zu interpretieren, da sich die Einflussfaktoren gegenseitig bedingen. Vielmehr empfiehlt sich, auf jeder Ebene bzw. Ausprägung des einen Faktors eine ANOVA für den jeweils anderen Faktor für die Testvariable zu rechnen (siehe nachfolgend A. und B.).
A.
Zum Beispiel wird zunächst jeweils für die beiden Geschlechter eine einfaktorielle ANOVA mit "Erfahrung" als Gruppenvariable und "Einkommen" als Testvariable gerechnet.
# A) Einfaktorielle ANOVA je Geschlecht
# bei signifikanter Interaktion (Geschlecht*Erfahrung)
data %>%
group_by(Geschlecht) %>%
anova_test(Einkommen ~ Erfahrung, effect.size = "pes")%>%
as.data.frame()
Der Output:
Geschlecht Effect DFn DFd F p p<.05 pes
1 Frau Erfahrung 3 109 33.174 2.59e-15 * 0.477
2 Mann Erfahrung 3 123 16.049 7.24e-09 * 0.281
Hier ist erkennbar, dass die p-Werte sehr klein sind und deutlich unter dem o.g. korrigierten Alpha-Niveau (0,025) liegen.
Die Erfahrung ist hier je Geschlecht ein signifikanter Einflussfaktor auf das Einkommen, also für Frauen (F(3,109) = 33.174, p < 0.001) als auch Männer (F(3,123) = 16.049; p < 0.001).
B.
Anschließend wird für die vier Erfahrungsstufen jeweils eine einfaktorielle ANOVA mit dem Geschlecht als Gruppenvariable und Einkommen als Testvariable gerechnet:
# B) Einfaktorielle ANOVA je Erfahrungsstufe
# bei signifikanter Interaktion (Geschlecht*Erfahrung)
data %>%
group_by(Erfahrung) %>%
anova_test(Einkommen ~ Geschlecht, effect.size = "pes")%>%
as.data.frame()
Der Output ist folgender:
Erfahrung Effect DFn DFd F p p<.05 pes
1 1 Geschlecht 1 58 6.373 1.40e-02 * 0.099
2 2 Geschlecht 1 61 35.891 1.21e-07 * 0.370
3 3 Geschlecht 1 59 1.384 2.44e-01 0.023
4 4 Geschlecht 1 54 4.015 5.00e-02 0.069
Hier zeigt sich, dass innerhalb der Erfahrungsstufen 1 (F(1,58) = 6.373; p < 0.001) und 2 ein Einkommensunterschied (F(1,61) = 35.891, p < 0.001) über die Geschlechter zeigt. In den Erfahrungsstufen 3 und 4 sind die Unterschiede relativ klein und demnach ist der p-Wert nicht hinreichend klein genug. Möglicherweise kann für einen Unterschied bei Erfahrungsstufe 4 argumentiert werden (vgl. Wasserstein, Lazar (2016)), da der p-Wert 0,05 ist - allerdings ist die Alphafehlerkorrektur hier noch zu bedenken.
6.1 Analytische post-hoc-Tests
Nun ist infolge der ANOVAs aus A. und B. jeweils eine Post-hoc-Analyse zu rechnen.
Es soll für A demnach geschaut werden, zwischen welchen Erfahrungsstufen je Geschlecht ein Unterschied besteht.
Hierfür wird das emmeans-Paket (estimated marginal means) verwendet und die Alphafehlerkorrektur mit Bonferroni vorgenommen.
Hinweis: Die Spalte des unkorrigierten p-Wertes wurde aus Gründen der Übersicht entfernt.
# Post-hoc-Analyse der ANOVAs aus A.
install.packages("emmeans")
library(emmeans)
data %>%
group_by(Geschlecht) %>%
emmeans_test(Einkommen ~ Erfahrung, p.adjust.method = "bonferroni") %>%
as.data.frame()
In der vorletzten Spalte ("p.adj") stehen die jeweiligen korrigierten p-Werte.
Geschlecht term .y. group1 group2 df statistic p.adj p.adj.signif
1 Frau Erf. Eink. 1 2 232 -0.214 1 e+ 0 ns
2 Frau Erf. Eink. 1 3 232 -5.92 6.96e- 8 ****
3 Frau Erf. Eink. 1 4 232 -6.80 5.36e-10 ****
4 Frau Erf. Eink. 2 3 232 -5.97 5.40e- 8 ****
5 Frau Erf. Eink. 2 4 232 -6.87 3.50e-10 ****
6 Frau Erf. Eink. 3 4 232 -1.05 1 e+ 0 ns
7 Mann Erf. Eink. 1 2 232 -3.34 5.81e- 3 **
8 Mann Erf. Eink. 1 3 232 -5.23 2.32e- 6 ****
9 Mann Erf. Eink. 1 4 232 -7.20 4.92e-11 ****
10 Mann Erf. Eink. 2 3 232 -1.65 6.07e- 1 ns
11 Mann Erf. Eink. 2 4 232 -3.62 2.17e- 3 **
12 Mann Erf. Eink. 3 4 232 -2.11 2.14e- 1 ns
Erkennbar ist, dass 8 der 12 paarweisen Vergleiche einen hinreichend kleinen p-Wert haben.
- Bei den Frauen unterscheiden sich die Einkommen zwischen den Erfahrungsstufen 1-3, 1-4, 2-3 und 2-4.
- Bei den Männern unterscheiden sich die Einkommen zwischen den Erfahrungsstufen 1-2, 1-3, 1-4 und 2-4.
6.2 Grafische Darstellungsmöglichkeiten
Die in 5.1 erzielte Erkenntnis kann zudem noch in einer Grafik dargestellt werden. Es eignen sich Liniendiagramme, besser noch Boxplots:
Hierzu wird der obige Code der post-hoc-Tests erneut verwendet und dessen Ergebnisse im Vektor ph gespeichert und dann lediglich in einen Boxplot übergeben
# Resultate speichern
ph <- data %>%
group_by(Geschlecht) %>%
emmeans_test(Einkommen~Erfahrung,
p.adjust.method = "bonferroni") %>%
add_xy_position(x = "Geschlecht")
# Resultate in einen Boxplot übergeben
ggboxplot(data, x = "Geschlecht", y = "Einkommen", color = "Erfahrung") +
stat_pvalue_manual(ph) +
labs(subtitle = get_test_label
(anova_test(data = data, Einkommen~Geschlecht*Erfahrung,
effect.size = "pes"), detailed = TRUE))
Das Ergebnis zeigt erneut je Geschlecht, wo Unterschiede zwischen den Erfahrungsstufen bestehen. Der besseren Lesbarkeit wegen auch mit Signifikanzindikatoren:

Die Darstellung kann nach gleichem Prinzip für Geschlechterunterschiede je Erfahrungsstufe vorgenommen werden:
# Resultate speichern
ph2 <- data %>%
group_by(Erfahrung) %>%
emmeans_test(Einkommen~Geschlecht,
p.adjust.method = "bonferroni") %>%
add_xy_position(x = "Erfahrung")
# Resultate in einen Boxplot übergeben
ggboxplot(data, x = "Erfahrung", y = "Einkommen", color = "Geschlecht") +
stat_pvalue_manual(ph2) +
labs(subtitle = get_test_label(
anova_test(data = data, Einkommen~Geschlecht*Erfahrung,
effect.size = "pes"), detailed = TRUE))

7 Videotutorial
8 Beispieldatensatz
Fiktiver Datensatz zum Download:
9 Literatur
- Blanca Mena, M. J., Alarcón Postigo, R., Arnau Gras, J., Bono Cabré, R., & Bendayan, R. (2017). Non-normal data: Is ANOVA still a valid option?. Psicothema, 2017, vol. 29, num. 4, p. 552-557.
- Field, Andy. Discovering statistics using IBM SPSS statistics. Sage, 2018.
- Hoff, T. (2021). The gender pay gap in medicine: a systematic review. Health Care Management Review, 46(3), E37-E49.
- Schrenker, Annekatrin, and Aline Zucco. "Gender Pay Gap steigt ab dem Alter von 30 Jahren stark an." Diw Wochenbericht 87.10 (2020): 137-145.
- Wasserstein, R. L., & Lazar, N. A. (2016). The ASA statement on p-values: context, process, and purpose. The American Statistician, 70(2), 129-133.


