Inhaltsverzeichnis
1 Ziel des Mann-Whitney-U-Test in SPSS
Der Mann-Whitney-U-Test ist ein nicht parametrischer “Mittelwertvergleich” bei 2 unabhängigen Stichproben. Er verwendet Ränge anstatt der tatsächlichen Werte, vergleicht also nicht wirklich Mittelwerte, sondern die zentralen Tendenzen der Gruppen. Er ist das Gegenstück zum t-Test bei zwei unabhängigen Stichproben, allerdings hat er nicht solche strengen Voraussetzungen.
- Nullhypothese: Es liegen keine Unterschiede bzgl. der zentralen Tendenz der beiden Gruppen vor.
- Alternativhypothese: Es liegen Unterschiede bzgl. der zentralen Tendenz der beiden Gruppen vor.
2 Voraussetzungen des Mann-Whitney-U-Test in SPSS
- zwei voneinander unabhängige Stichproben/Gruppen
- ordinal oder metrisch skalierte y-Variable
- normalverteilte y-Variable innerhalb der Gruppen nicht nötig
3 Durchführung des Mann-Whitney-U-Test in SPSS
Über das Menü in SPSS: Analysieren -> Nichtparametrische Test -> Alte Dialogfelder -> 2 unabhängige Stichproben
Als Testvariable ist die zu testende Variable einzusetzen. Die Gruppierungsvariable ist die Variable, die die Gruppen unterscheidet. Im Beispiel testen wir untrainierte (Gruppe 0) und trainierte Menschen (Gruppe 2) auf Unterscheide hinsichtlich ihres Ruhepulses.
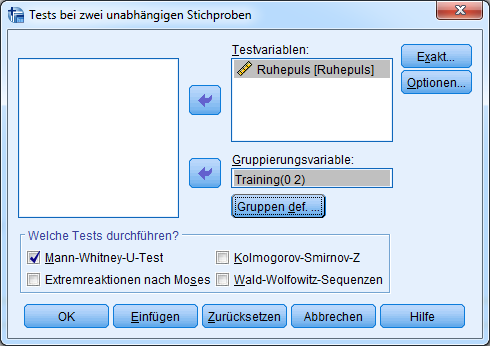
Als Test muss der Mann-Whitney-U-Test ausgewählt werden. Zusätzlich sollte unter Optionen noch “Deskriptive Statistik” ausgewählt werden.
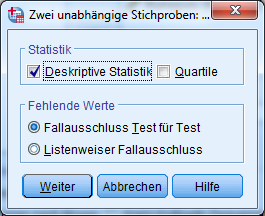
Ein Klick auf “OK” führt die Berechnung durch und zeigt die Ergebnisse an.
4 Interpretation des Mann-Whitney-U-Test in SPSS
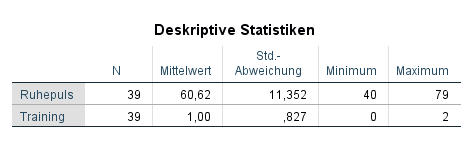
Die deskriptiven Statistiken geben lediglich einen kurzen Überblick, wie der Ruhepuls und das Training ausgeprägt sind. Mittelwert, Standardabweichung, Minimum und Maximum werden angezeigt. Hinweis: Hier steht bei n=39. Das liegt daran, dass noch eine weitere Gruppe im Datensatz existiert, die aber bei der folgenden Analyse nicht verwendet wird. Demzufolge sind in folgender Tabelle 2×13 = 26 Beobachtungen vorhanden.
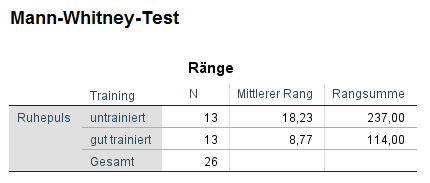
Da der Mann-Whitney-U-Test mit Rängen arbeitet, werden für die beiden Gruppen “untrainiert” und “gut trainiert” die mittleren Ränge und die Rangsumme angezeigt. Es ist bereits erkennbar, dass die untrainierte Gruppe einen höheren mittleren Rang (18,23 vs. 8,77) und eine höhere Rangsumme (237 vs. 114) hat – verglichen mit der Gruppe der gut Trainierten.
Allerdings ist hiermit noch nicht gesagt, ob es tatsächlich einen statistisch signifikanten Unterschied gibt. Hierzu braucht es den Mann-Whitney-U-Test und dessen Ergebnisse.
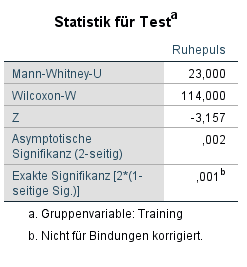
Die Tabelle zeigt in der vorletzten Zeile die “Asymptotische Signifikanz (2-seitig)” von 0,002. Wenn beide Gruppen zusammen genommen mehr als 40-50 Fälle aufweisen, wird diese verwendet. Bei weniger als 50 (hier 26) sollte die exakte Signifikanz betrachtet werden! (Field(2019), S. 296)
Die exakte Signifikanz ist (ebenso wie die asymptotische) kleiner als die Verwerfungsgrenze von Alpha=0,05 und reicht somit zur Verwerfung der Nullhypothese von gleichen Ruhepulsen über die Gruppen hinweg. Demzufolge wird die Alternativhypothese angenommen, dass über die Gruppen hinweg unterschiedliche Ruhepulse existieren.
ACHTUNG: Wenn bereits eine Wirkungsvermutung vor dem Test existiert – die plausible Annahme, dass ein besser trainierter Mensch einen niedrigeren Ruhepuls hat, wäre so eine – dann würde man 1-seitig testen. Hierzu darf die Asymptotische bzw. Exakte Signifikanz halbiert werden und erneut mit 0,05 verglichen werden. In diesem Falle ändert sich entsprechend nichts an der Aussage der Verwerfung der Nullhypothese.
5 Ermittlung der Effektstärke des Mann-Whitney-U-Tests
Die Effektstärke r wird mit folgender Formel berechnet. Der z-Wert wird durch die Wurzel der Stichprobengröße geteilt. Aufgrund der Betragsstriche wird dieser Quotient immer positiv sein.
![Rendered by QuickLaTeX.com \[ r = \lvert \frac{z}{\sqrt{N}}\rvert= \lvert \frac{-3,157}{\sqrt{26}} \rvert=0,619 \]](https://bjoernwalther.com/wp-content/ql-cache/quicklatex.com-efb207b146cf029b88a3f396b6c044ad_l3.png)
Im Beispiel ist also -3,157 durch die Wurzel aus 26 zu teilen und der Betrag dessen zu nehmen. Das Ergebnis hieraus lautet: 0,619.
Laut Cohen: Statistical Power Analysis for the Behavioral Sciences (1988), S. 79-81 bzw. Cohen (1992), S 157 sind die Effektgrenzen
- ab 0,1 (schwach),
- ab 0,3 (mittel) und
- ab 0,5 (stark).
Im vorliegenden Beispiel ist die Effektstärke mit 0,619>0,5 stark. Es handelt sich also um einen starken Effekt hinsichtlich des Unterschiedes des Ruhepulses von Untrainierten verglichen mit (gut) Trainierten.
6 Reporting
Zum Berichten empfiehlt sich die Angabe der Gruppenmediane, der U-Statistik mitsamt der Gruppengrößen, der z-Statistik sowie dem p-Wert. Bei signifikanten Unterschieden ist zudem die Effektstärke r zu berichten und einzuordnen:Untrainierte Probanden (Mdn = 69) haben gegenüber trainierten Probanden (Mdn = 52) einen signifikant höheren Ruhepuls, U (N1=13, N2=13) = 23; z = -3,157; p = 0,001; r = 0,619. Nach Cohen (1988/1992) ist dieser Unterschied groß.
7 Videotutorial
Fragen können unter dem verlinkten Video gerne auf YouTube gestellt werden.
8 Literatur
- Cohen, Jacob. “A power primer.” Psychological bulletin 112.1 (1992): 155.
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences: Jacob Cohen. New York, N.J: Psychology Press.
- Field, A. P. (2019). Discovering statistics using IBM SPSS statistics.
- Mann, H. B., & Whitney, D. R. (1947). On a test of whether one of two random variables is stochastically larger than the other. The annals of mathematical statistics, 50-60.
Weitere nützliche Tutorials findest du auf meinem YouTube-Kanal.


