Cook Distanz in R ermitteln und interpretieren – Ausreißer erkennen

1 Prinzip der Cook Distanzen – einflussreiche Fälle erkennen

Mit der Cook-Distanz in R (folgend manchmal auch Cook’s Distance) kann man einflussreiche Fälle, u.a. im Rahmen einer multiplen linearen Regression identifizieren. Mitunter nennt man diese Fälle auch Ausreißer. Im Prinzip sind es aber für die Stichprobe ungewöhnliche Kombinationen von x-Variablen und y-Variable, die grafisch gesprochen (deutlich) außerhalb der Punktewolke liegen.

Im Beispieldiagramm sind die roten Dreiecke deutlich von der Punktewolke (grüne Datenpunkte) entfernt. Es ist einmal eine sehr große und leichte Person (rechts unten), und einmal eine sehr kleine und schwere Person (links oben) – gleichzeitig ist erkennbar, dass große und schwere Personen oder kleine und leichte Personen nichts ungewöhnliches für diese Stichprobe sind.

Bei den ungewöhnlichen Fällen (auch „Fälle mit Hebelwirkung“ genannt) wird die blaue (beste) Regressionsgerade jeweils in deren Richtung gehebelt, was jeweils die rote Regressionsgerade bedeuten würde. Diese passt jeweils deutlich schlechter für alle anderen Datenpunkte als vorher, was das Modell z.T. erheblich verschlechtern kann. Folglich ist es wünschenswert, solche Fälle zu identifizieren und über das weitere Vorgehen zu diskutieren.

 

2 Ermitteln der Cook-Distanz in R

Zunächst wird ganz normal eine (multiple) lineare Regression gerechnet.

Im Beispiel möchte ich den Abiturschnitt mit den unabhängigen Variablen Motivation und Intelligenzquotient prognostizieren.

model <- lm(Abischni ~ IQ + Motivation, data = df)

Auf Basis dieses Modells und dessen Berechnung sind schon alle weiteren Grundlagen für die nächsten Schritte vorhanden.
 

2.1 Grafische Darstellung der Cook-Distanzen in R

Hierzu verwendet man das berechnete Modell in Verbindung mit der plot()-Funktion und dem Argument "4" wie folgt:

plot(model, 4)

 
Im Ergebnis erhält man bereits einen sehr aufschlussreichen Plot. Auf der x-Achse werden die Fallnummern abgetragen und auf der y-Achse die Cook-Distanzen.

 

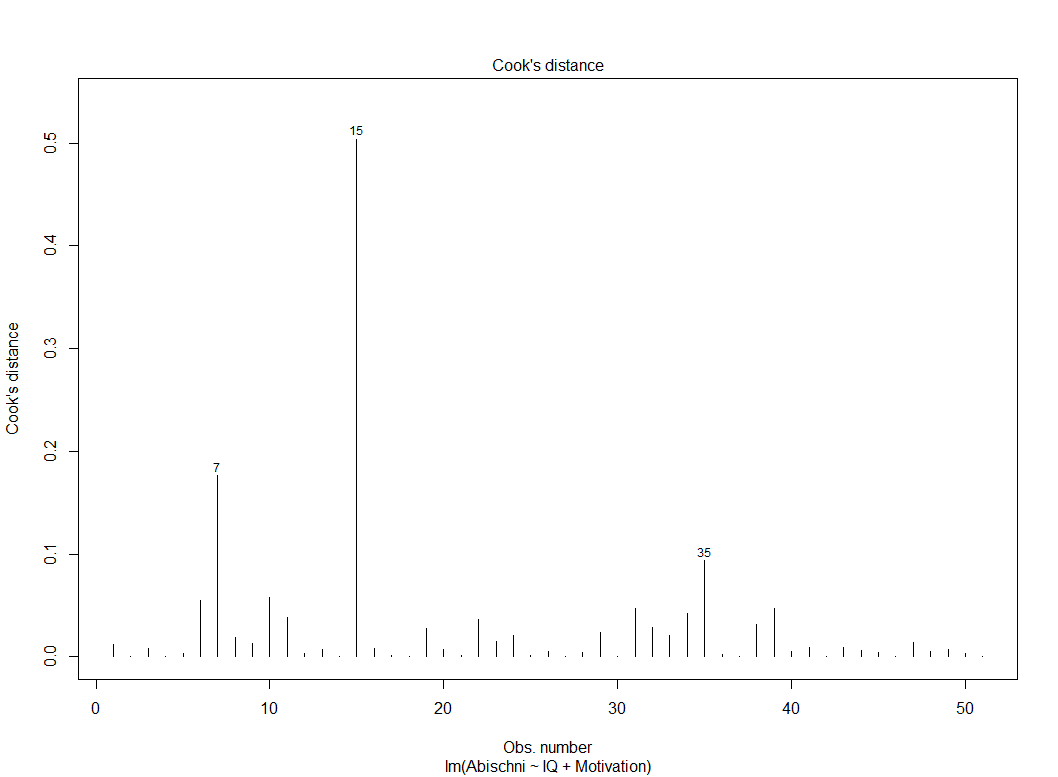
Hier fällt bereits auf, dass einige Fälle verhältnismäßig für diese Stichprobe sehr große Cook-Distanzen haben. Diese sind auch beschriftet und lauten absteigend nach der Cook-Distanz: 15, 7 und 35. Aufgrund dessen mag es bereits hilfreich sein, sich diese Fälle genauer anzuschauen. Interessant sind dabei nur die entsprechenden unabhängigen Variablen sowie die abhängige Variable. Dazu komme ich aber später noch. Vorher zeige ich die exakte Berechnung der Cook-Distanzen.

 

2.2 Berechnung der Cook-Distanzen in R

Die Cook-Distanzen lassen sich in R mit der cooks.distance()-Funktion berechnen und mit der View()-Funktion anzeigen:

cd <- cooks.distance(model)
View(cd)

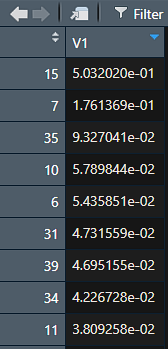
Ich habe hier bereits eine absteigende Sortierung vorgenommen und man kann die drei Fälle mit den höchsten Cook-Distanzen ganz oben erkennen. Die Fall-Nummern sind zudem mit angegeben: 15 (0.5032), 7 (0.1761) und 35 (0.0933).

Hinweis: 5.032e-01 ist die wissenschaftliche Schreibweise für 0.5032

 

3 Interpretation der Cook-Distanzen

Wie bereits erwähnt, dient die Cook-Distanz zur Identifikation von einflussreichen Fällen/Fällen mit großer Hebelwirkung.

Hierzu gibt es 3 Zugänge:
 

3.1 Zugang 1 und 2 - feste und halbfeste Grenzen

1) Cook, R., & Weisberg, S. (1982). Criticism and Influence Analysis in Regression. Sociological Methodology, 13, 313-361. sprechen von einer Grenze von 1. Sind also Cook Distanzen unter 1, existieren keine einflussreichen Fälle.

2) Hardin, J. W., & Hilbe, J. M. (2007). Generalized linear models and extensions, S. 49. bezeichnen Werte, die über 4/n liegen als problematisch. n ist hierbei die Stichprobengröße. Im Falle meiner Stichprobe mit 51 Fällen wäre der errechnete Grenzwert 0.078. Offensichtlich wird mit einer zunehmenden Stichprobengröße diese Grenze immer kleiner. Das kann zu Problemen führen, weswegen man die unten beschriebene dritte Variante in Betracht ziehen sollte.

Zunächst noch der Code für die beiden eben beschriebenen Methoden:

#Feste Grenze
View(cd<1)

#Halbfeste Grenze
View(cd < 4/51)

Im nachfolgenden Output wird mit TRUE und FALSE angegeben, ob die Werte unter der Grenze liegen. Hier zeige ich nur für die zweite Methode (halbfeste Grenze) einen Ausschnitt.
(Methode 1 zeigt nur TRUE):

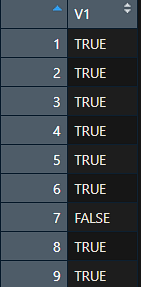
Fall 7 wird mit FALSE beschriftet. Die gesetzte Grenze von (4/51 = 0,078) wird überschritten. Ein Grund für Ausschluss ist das allerdings nicht unbedingt, wie wir noch sehen werden.

 

3.2 Zugang 3 - Verhältnismäßigkeit

Bei diesem Zugang gibt es keine festen oder variablen Grenzen. Vielmehr betrachtet man die Cook-Distanzen in Relation zueinander. Hierbei hilft der erneute Blick auf obiges Streudiagramm deutlich mehr als auf die nackten Zahlen zu schauen.

Hier ist erkennbar, dass Fall 7 und besonders Fall 15 eine verhältnismäßig große Cook-Distanz haben. Das war auch anhand der Werte schon erkennbar, dass die Distanzen 0.17614 (Fall 7) und 0.53382 (Fall 15) deutlich größer als der Rest sind. Diese Fälle stechen aber nun sehr deutlich hervor und sollten noch mal etwas näher betrachtet werden, anstatt sie direkt blind auszuschließen. Schüler 15 scheint etwas zu schlecht, Schüler 7 etwas zu gut.

 

Die Werte sind folgende:

ID	Abitur Tatsächlich	Motivation	IQ
15	3,4	8	97
7	2	8	100

 

Diskussion

Beim Durchscrollen des Datensatzes fällt insbesondere auf, dass Schüler mit einer hohen Motivation von 3 häufig einen deutlich besseren Abiturschnitt haben. Der Schüler mit ID 15 hat einen Schnitt von 3,4. Der "zweitschlechteste" Schüler mit einer Motivation von 3 (höchste Ausprägung) hat einen Abiturschnitt von 2,2. Zwar spielt die Intelligenz auch eine nicht vernachlässigbare Rolle, allerdings haben im Datensatz motivierte Schüler mindestens einen IQ von 115 und damit per se eine bessere Grundveranlagung für gute schulische Leistungen. Man würde also eher einen höheren IQ und ein bessere Abiturnote für diese vergleichsweise hohe Motivation erwarten.

Warum hat Schüler mit ID 7 ebenfalls eine hohe Cook-Distanz? Hier ist die Motivation ebenfalls hoch, das Abitur entsprechend gut. Hier spielt vor allem der IQ eine Rolle. Die Grundveranlagung ist mit einem IQ von 100 zwar prinzipiell gegeben, allerdings schätzt das Modell auf Basis der vorliegenden Daten mit einem eher durchschnittlichen IQ die tatsächliche Note deutlich niedriger ein. Somit ist die tatsächliche Note besonders aufgrund des IQ's zu hoch als erwartet werden würde.

 

4 Fazit - Ausreißer, oder nicht?

Bevor diese Frage beantwortet werden kann, muss die Frage gestellt werden, ob bei der Messung und Datenerfassung kein Fehler vorliegt. Vielleicht hat der Schüler mit der ID 15 ja ein Abitur von 2,4 statt 3,4 - ein Tippfehler bei der Erfassung ist denkbar. Oder aber der Schüler mit der ID 7 hat einen IQ von 110 und demzufolge wäre das gute Abitur für das Modell auch wieder plausibler. Wie aber nun weiter?

Aufgrund der vorliegenden Daten und der deutlichen Abweichung der tatsächlichen und geschätzten Werte können die zwei obigen Fälle sicherlich als ungewöhnliche Fälle (für die Stichprobe!) klassifiziert werden. Ist das ein Grund, sie auszuschließen?
Nicht unbedingt. Sind keine Mess- oder Erhebungsfehler ersichtlich bzw. wurden die Werte erneut auf Plausibilität geprüft und es konnte kein Fehler festgestellt werden, dann ist ein Ausschluss sehr schwer möglich. Hierfür gibt es schlicht keine Argumente.

Nur, weil die Beobachtungen anders als die Masse sind, ist das kein Grund sie auszuschließen - das Motto "was nicht passt, wird passend gemacht" ist hier fehl am Platz. Eine Diskussion, warum diese Fälle ungewöhnlich sind, ist viel zielführender, besonders im Hinblick auf Folgeuntersuchungen, wo auch Ausreißer auftreten können.

 

4 Videotutorial

 

5 Datensatz zum Download

 

6 Literatur

• Cook, R., & Weisberg, S. (1982). Criticism and Influence Analysis in Regression. Sociological Methodology, 13, 313-361.
• Hardin, James W., and Joseph M. Hilbe. Generalized linear models and extensions. Stata press, 2007.