1 Zweck des Bland-Altman-Plots
Ein Bland-Altman-Plot vergleicht zwei Messmethoden miteinander. Zumeist gibt es eine etablierte Methode, die sehr genau ist und als “Goldstandard” bezeichnet wird. Diese Methode kann aber langsam, teuer usw. sein, weswegen man eine schnellere, günstigere Methode entwickelt. Die Frage, die in dem Zusammenhang zu beantworten ist: Ist die neue Methode in etwa genauso gut, wie die alte?
Den grundlegenden Aufbau und die Logik dahinter habe ich bereits in einem separaten Artikel erklärt.
2 Bland-Altman-Plot in SPSS erstellen
2.1 Vorarbeiten
2.1.1 Berechnung von Differenz und Mittelwert
Für ein Bland-Altman-Plot in benötigt man die gleichen Probanden bzw. Testobjekte für beide Messungen. Beide Messmethoden A und B müssen zwingend am selben Proband/Testobjekt durchgeführt werden und in verschiedenen Variablen hinterlegt sein.
Somit erhält man zwei Messreihen, jeweils eine für Messmethode A und B. Das kann exemplarisch wie folgt aussehen:
Messung_A Messung_B
23,8957 24,2252
20,5800 20,2460
23,9141 23,7824
23,6897 24,1744
26,1851 27,2627
24,9698 25,5445
21,4119 23,4075
24,0488 25,2615
29,5131 30,7412
24,1463 25,5308
... ...
Zunächst benötigt man zwei weitere Variablen. Zum einen die Differenz zwischen den beiden Messungen und zum anderen den Mittelwert der beiden Messungen.
1) Das kann man entweder über Transformieren -> Variable berechnen:
2) Ein anderer Weg wäre direkt über die Syntax – die beiden Variablen heißen “Messung_A” und “Messung_B”:
COMPUTE Differenz=Messung_A - Messung_B.
COMPUTE Mittelwert=MEAN(Messung_A,Messung_B).
EXECUTE.
2.1.2 Prüfung der Normalverteilung der Differenz
Eine Voraussetzung für den Bland-Altman-Plot ist die Normalverteilung der Differenz der beiden Messreihen.
Ausführlich zeigt dieser Artikel die Prüfung auf Normalverteilung.
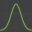
Am einfachsten wird mit einem Histogramm auf in etwa Normalverteilung geprüft.
1) Ein erster Weg ist über Grafik -> Diagramm erstellen:
2) Ein zweiter Weg ist über die Syntax – die abzutragende Variable heißt “Differenz”:
* Diagrammerstellung.
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=Differenz MISSING=LISTWISE REPORTMISSING=NO
/GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
SOURCE: s=userSource(id("graphdataset"))
DATA: Differenz=col(source(s), name("Differenz"))
GUIDE: axis(dim(1), label("Differenz"))
GUIDE: axis(dim(2), label("Häufigkeit"))
GUIDE: text.title(label("Einfaches Histogramm von Differenz"))
ELEMENT: interval(position(summary.count(bin.rect(Differenz))), shape.interior(shape.square))
END GPL.
Im Ergebnis erhält man in meinem Beispiel folgendes Histogramm, was in etwa eine Normalverteilung darstellt. Somit kann mit der Erstellung fortgefahren werden.
2.2 Erstellung eines einfachen Bland-Altman-Plots
2.2.1 Ausgangspunkt Streudiagramm
Nach dem Abschluss aller Vorarbeiten wird das Diagramm erstellt. Die Basis stellt ein Streudiagramm dar.
1) Hierzu geht es erneut über Grafik -> Diagramm erstellen:
2) Die zweite Möglichkeit geht erneut über die Syntax. Die Variablen heißen in meinem Falle “Mittelwert” und “Differenz”.
* Diagrammerstellung.
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=Mittelwert Differenz MISSING=LISTWISE REPORTMISSING=NO
/GRAPHSPEC SOURCE=INLINE
/FITLINE TOTAL=NO SUBGROUP=NO.
BEGIN GPL
SOURCE: s=userSource(id("graphdataset"))
DATA: Mittelwert=col(source(s), name("Mittelwert"))
DATA: Differenz=col(source(s), name("Differenz"))
GUIDE: axis(dim(1), label("Mittelwert"))
GUIDE: axis(dim(2), label("Differenz"))
GUIDE: text.title(label("Streudiagramm von Differenz Schritt: Mittelwert"))
ELEMENT: point(position(Mittelwert*Differenz))
END GPL.
Das sieht dann zunächst wie folgt aus:
2.2.2 Schwankungsbereich einzeichnen
Der Titel und die Achsenbeschriftungen werden später angepasst. Wichtig ist jetzt die akzeptable Schwankungsbreite bzw. die Geraden, die jene definieren.
Hierzu ist es notwendig Mittelwert und Standardabweichung von der Variable “Differenz” der beiden Messmethoden zu ermitteln.
1) Entweder kann man mit einem Rechtsklick auf die Variable Differenz die “Deskriptiven Statistiken” anfordern.
2) Oder man bemüht die Syntax. Die Variable heißt in meinem Falle “Differenz”.
FREQUENCIES VARIABLES=Differenz
/STATISTICS=RANGE MINIMUM MAXIMUM STDDEV MEAN MEDIAN
/FORMAT=NOTABLE
/ORDER=ANALYSIS.
Das führt dann in meinem Beispiel zu folgender Ausgabe:
Wichtig sind die folgenden Werte:
- Mittelwert = -0,7393
- Standardabweichung = 0,741564
Nun wird auf den Mittelwert die 1,96-fache Standardabweichung addiert bzw. von Mittelwert abgezogen:
- Oberer Toleranzbereich: -0,7393 + 1,96*0,741564 = 0,714
- Unterer Toleranzbereich: -0,7393 – 1,96*0,741564 = -2,192
An diesen beiden y-Werten sind nun die Begrenzungen des Schwankungsbereiches einzuzeichnen.
Dazu klickt man doppelt auf das Streudiagramm und wählt im oberen Bereich den Button “Eine Bezugslinie zur y-Achse hinzufügen“.
Als Nächstes wird im Reiter “Bezugslinie” bei Position zunächst der obere Toleranzbereich (0,714) eingegeben und im Reiter “Linien” ein anderes Design jener ausgewählt. Exemplarisch hier grün und gestrichelt.
Dies wiederholt man für den unteren Toleranzbereich (-2,192) als auch den Mittelwert (-0,7393) und erhält abschließend nachfolgendes Bland-Altman-Diagramm:
3 Interpretation des Bland-Altman-Plots
Ich hatte bereits eingangs auf einen ausführlichen Artikel hierzu verwiesen. Deshalb an dieser Stelle nur die wichtigsten Informationen.
Die Frage nach einer annehmbaren Abweichung muss primär beantwortet werden. Bestenfalls befinden sich keine Punkte ober- bzw. unterhalb der Abweichungstoleranz. Dies ist im Beispiel der Fall. Vereinzelte Fälle außerhalb können vorkommen, sollten aber hinsichtlich möglicher Messfehler noch mal geprüft werden. Können Messfehler ausgeschlossen werden, ist zu prüfen, welche Umstände zu einem anderen Messergebnis geführt haben. Können diese repliziert und damit künftig für eine solche Abweichung kontrolliert werden, kann das Messverfahren angepasst werden bzw. auf die Umstände für ungenaue Messungen in den Instruktionen hingewiesen werden.
4 Videotutorial
https://www.youtube.com/watch?v=ocRASWBUxjc/
5 Literatur
Bland, J. M., & Altman, D. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. The Lancet, 327(8476), 307-310.